题目内容
等比数列{an}中.a1,a2,a3分别是下表第一、二、三行中的某一个数.且a1•a2•a3中的任何两个数不在下表的同一列.| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(Ⅱ)如数列{bn}满足bn=an+(-1)lnan,求数列bn的前n项和sn.
【答案】分析:(Ⅰ)由表格可看出a1,a2,a3分别是2,6,18,由此可求出{an}的首项和公比,继而可求通项公式
(Ⅱ)先写出bn发现bn由一个等比数列、一个等差数列乘(-1)n的和构成,故可分组求和.
解答:解:(Ⅰ)当a1=3时,不合题意
当a1=2时,当且仅当a2=6,a3=18时符合题意
当a1=10时,不合题意
因此a1=2,a2=6,a3=18,所以q=3,
所以an=2•3n-1.
(Ⅱ)bn=an+(-1)nlnan
=2•3n-1+(-1)n[(n-1)ln3+ln2]
=2•3n-1+(-1)n(ln2-ln3)+(-1)nnln3
所以sn=2(1+3+…+3n-1)+[-1+1-1+1+…+(-1)n](ln2-ln3)+[-1+2-3+4-…+(-1)nn]ln3
所以当n为偶数时,sn= =
=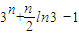
当n为奇数时,sn=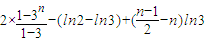 =
=
综上所述sn=
点评:本题考查了等比数列的通项公式,以及数列求和的方法,只要简单数字运算时不出错,问题可解,是个中档题.
(Ⅱ)先写出bn发现bn由一个等比数列、一个等差数列乘(-1)n的和构成,故可分组求和.
解答:解:(Ⅰ)当a1=3时,不合题意
当a1=2时,当且仅当a2=6,a3=18时符合题意
当a1=10时,不合题意
因此a1=2,a2=6,a3=18,所以q=3,
所以an=2•3n-1.
(Ⅱ)bn=an+(-1)nlnan
=2•3n-1+(-1)n[(n-1)ln3+ln2]
=2•3n-1+(-1)n(ln2-ln3)+(-1)nnln3
所以sn=2(1+3+…+3n-1)+[-1+1-1+1+…+(-1)n](ln2-ln3)+[-1+2-3+4-…+(-1)nn]ln3
所以当n为偶数时,sn=
 =
=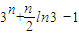
当n为奇数时,sn=
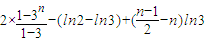 =
=
综上所述sn=

点评:本题考查了等比数列的通项公式,以及数列求和的方法,只要简单数字运算时不出错,问题可解,是个中档题.

练习册系列答案
相关题目