题目内容
已知数列 ,
,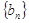 分别为等比,等差数列,数列
分别为等比,等差数列,数列 的前n项和为
的前n项和为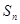 ,且
,且 ,
, ,
, 成等差数列,
成等差数列,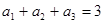 ,数列
,数列 中,
中,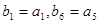 ,
,
(Ⅰ)求数列 ,
,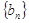 的通项公式;
的通项公式;
(Ⅱ)若数列 的前n项和为
的前n项和为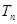 ,求满足不等式
,求满足不等式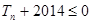 的最小正整数
的最小正整数 。
。
(Ⅰ) ,
,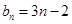 ;(Ⅱ)满足不等式
;(Ⅱ)满足不等式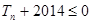 的最小正整数
的最小正整数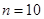 .
.
解析试题分析:(Ⅰ)已知数列 为等比数列,数列
为等比数列,数列 的前n项和为
的前n项和为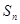 ,且
,且 ,
, ,
, 成等差数列,由
成等差数列,由 ,
, ,
, 成等差数列,需用前
成等差数列,需用前 项和解题,需讨论
项和解题,需讨论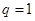 与
与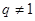 两种情况,当
两种情况,当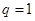 不符合题意,故
不符合题意,故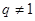 ,由前
,由前 项和公式求出
项和公式求出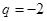 ,再由
,再由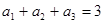 求出
求出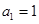 ,从而得
,从而得 的通项公式,求数列
的通项公式,求数列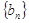 的通项公式,由
的通项公式,由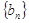 为等差数列,
为等差数列,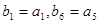 ,分别求出
,分别求出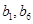 ,从而得到
,从而得到 ,可写出
,可写出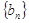 的通项公式;(Ⅱ)若数列
的通项公式;(Ⅱ)若数列 的前n项和为
的前n项和为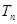 ,求满足不等式
,求满足不等式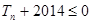 的最小正整数
的最小正整数 ,首先求出
,首先求出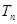 ,而数列
,而数列 ,是由一个等差数列与一个等比数列对应项积所组成的数列,可用错位相减法求
,是由一个等差数列与一个等比数列对应项积所组成的数列,可用错位相减法求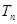 ,得
,得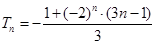 ,让
,让 ,即
,即 ,解出
,解出 的范围,可得
的范围,可得 的最小值.
的最小值.
试题解析:(Ⅰ) ,
, ,
, 成等差数列
成等差数列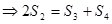
①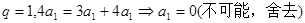
②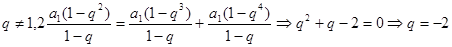
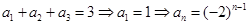 ,
,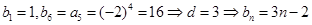 (6分)
(6分)
(Ⅱ)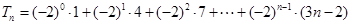 ,
,  ,两式相减得到
,两式相减得到 ,
, ,
, ,故满足不等式
,故满足不等式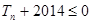 的最小正整数
的最小正整数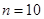 .(12分)
.(12分)
考点:等差数列与等比数列的通项公式,数列求和.

练习册系列答案
相关题目
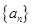 的前
的前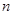 项和为
项和为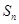 ,且
,且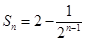 .
.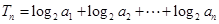 ,求证:
,求证: .
.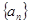 中,
中,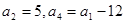 .
.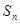 取最大值时求
取最大值时求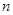 的值.
的值.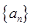 是首项为
是首项为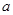 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前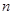 项和.
项和. ,
, ,求数列
,求数列 ,
, ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.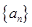 的前
的前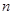 项和为
项和为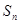 ,公差
,公差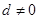 ,
,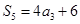 ,且
,且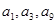 成等比数列.
成等比数列.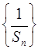 的前
的前 的前
的前 项和为
项和为 ,且
,且 是
是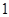 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,证明:
,证明: .
.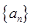 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*. 为何值时,数列
为何值时,数列 是数列
是数列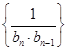 的前
的前 项和,求
项和,求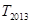 的值.
的值. 为等差数列,且
为等差数列,且 ,
, 为
为 项和.
项和. 及
及 ,求数列
,求数列 的通项公式
的通项公式 及其前
及其前 .
. 是首项为1,公差为
是首项为1,公差为 的等差数列,数列
的等差数列,数列 是首项为1,公比为
是首项为1,公比为 的等比
的等比 ,
, ,求数列
,求数列 的前
的前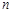 项和;
项和; ,使得
,使得 .试比较
.试比较 与
与 的大小,并说明理由.
的大小,并说明理由.