题目内容
数列 的前
的前 项和为
项和为 ,且
,且 是
是 和
和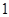 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
(1)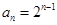 ,
,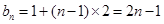 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
解析试题分析:本题主要考查等差数列与等比数列的概念、通项公式、前 项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用
项和公式、数列求和等基础知识,考查运算能力、推理论证能力.第一问,先利用 是
是 和
和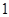 的等差中项,得到
的等差中项,得到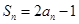 ,由
,由 求
求 ,注意
,注意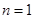 的情况,不要漏掉,会得到
的情况,不要漏掉,会得到 为等比数列,利用等比数列的通项公式,求和公式直接写出
为等比数列,利用等比数列的通项公式,求和公式直接写出 和
和 ,再利用已知求出
,再利用已知求出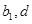 ,写出等差数列的通项公式;第二问,先化简
,写出等差数列的通项公式;第二问,先化简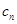 表达式,利用裂项相消法求和求
表达式,利用裂项相消法求和求 ,利用放缩法比较
,利用放缩法比较 与
与 的大小,作差法判断数列的单调性,因为数列
的大小,作差法判断数列的单调性,因为数列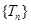 为递增数列,所以最小值为
为递增数列,所以最小值为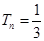 ,即
,即 ,所以
,所以 .
.
试题解析:(1)∵ 是
是 和
和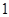 的等差中项,∴
的等差中项,∴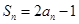
当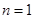 时,
时,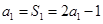 ,∴
,∴
当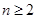 时,
时,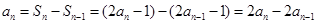 ,
,
∴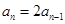 ,即
,即 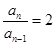 3分
3分
∴数列 是以
是以 为首项,
为首项,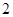 为公比的等比数列,
为公比的等比数列,
∴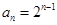 ,
, 5分
5分
设 的公差为
的公差为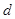 ,
, ,
,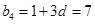 ,∴
,∴
∴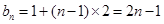 6分
6分
(2) 7分
7分
∴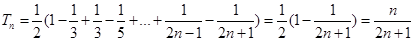 9分
9分
∵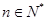 ,∴
,∴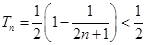 10分
10分
∴数列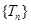 是一个递增数列 ∴
是一个递增数列 ∴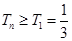 .
.
综上所述, 12分
12分
考点:1.等差中项;2.由 求
求 ;3.等比、等差数列的通项公式与求和公式;4.裂项相消法求和.
;3.等比、等差数列的通项公式与求和公式;4.裂项相消法求和.

练习册系列答案
相关题目
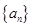 的前3项和
的前3项和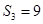 ,且
,且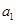 、
、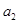 、
、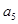 成等比数列.
成等比数列.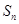 ;
;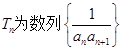 的前n项和,证明:
的前n项和,证明: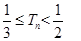 ;
; ,若
,若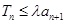 对一切
对一切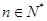 恒成立,求实数
恒成立,求实数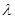 的最小值.
的最小值.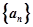 的前n项和为
的前n项和为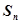 ,且
,且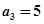 ,
, .
. 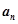 ;
; ,求数列
,求数列 的前n项和
的前n项和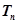 .
.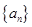 为等差数列,且
为等差数列,且 .
.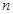 项和
项和 ;
; 满足
满足 求数列
求数列 ,
,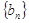 分别为等比,等差数列,数列
分别为等比,等差数列,数列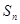 ,且
,且 ,
, ,
, 成等差数列,
成等差数列,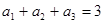 ,数列
,数列 中,
中,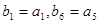 ,
, 的前n项和为
的前n项和为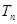 ,求满足不等式
,求满足不等式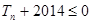 的最小正整数
的最小正整数 。
。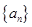 满足
满足 ,
, .
. 的前n项和.
的前n项和. 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列 项和为
项和为 ,且满足
,且满足
 项和
项和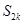 ;
;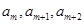 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数 的值;若不存在,说明理由
的值;若不存在,说明理由 的首项
的首项 ,公差
,公差 .且
.且 分别是等比数列
分别是等比数列 的
的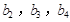 .
.  与
与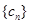 对任意自然数
对任意自然数 均有
均有 …
… 成立,求
成立,求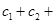 …
… 的值.
的值.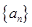 满足
满足 (
( 为常数),
为常数),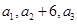 成等差数列.
成等差数列. 满足
满足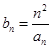 ,证明:
,证明: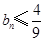 .
.