题目内容
9.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x>0时,g(1)=0且f′(x)•g(x)+f(x)•g′(x)>0,则 不等式g(x)•f(x)>0的解集是( )| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
分析 构造函数m(x)=f(x)•g(x),根据导数和函数单调性之间的关系,判断函数m(x)的单调性,结合函数的奇偶性的性质即可得到结论.
解答 解:设m(x)=f(x)•g(x),
∵x>0时,f′(x)g(x)+f(x)g′(x)>0,
即m′(x)=[f(x)g(x)]′>0
故m(x)在x>0时递增,
∵f(x)、g(x)分别是定义在R上的奇函数和偶函数,
∴m(x)=f(x)g(x)是R上的奇函数,
∴m(x)的图象关于原点对称,
即m(x)在x<0时也是增函数.
∵g(1)=0,∴g(-1)=-g(1)=0,
∴m(-1)=0且m(1)=0,则函数m(x)对应的草图为
则m(x)>0的解为:x>1或-1<x<0.
故不等式的解集为{x|x>1或-1<x<0},
故选:B
点评 本题考查了函数的奇偶性的应用,以及导数的运算,不等式的解法等,根据导数的正负可以确定函数的单调性,利用数形结合的思想进行解题.属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
20.等差数列{an}的前n项和为Sn,已知S11=121,则a6=( )
| A. | 1 | B. | 110 | C. | 11 | D. | 132 |
14.已知a>0,b>0,a+$\frac{1}{a}$+$\frac{b}{2}$+$\frac{8}{b}$=6,若直线y=mx+ab与不等式组$\left\{\begin{array}{l}x+y-3≥0\\ 2x-y≥0\\ x-2≤0\end{array}\right.$,表示的平面区域有公共点,则实数m的取值范围是( )
| A. | $[{-6,-\frac{3}{2}}]$ | B. | [-2,0] | C. | $[{-2,-\frac{3}{2}}]$ | D. | (-∞,-2] |
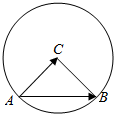 如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.
如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.