题目内容
6.已知动点P在抛物线y2=2x上,定点A(m,0)(m>0),求|PA|的最小值以及取最小值时P点的横坐标.分析 先设P点坐标为(x,y),利用两点间的距离公式求出点P与点A的距离的表达式;再结合二次函数在固定区间上的最值求法即可求出点P与点A的距离的最小值,并求得P点横坐标.
解答 解:设P(x,y),则$|PA|=\sqrt{(x-m)^{2}+{y}^{2}}$=$\sqrt{{x}^{2}-2mx+{m}^{2}+2x}$=$\sqrt{{x}^{2}+(2-2m)x+{m}^{2}}$,x∈(0,+∞),
设函数g(x)=x2+(2-2m)x+m2,(x∈(0,+∞)),
其对称轴方程为x=m-1,
当m-1<0,即m<1时,
g(x)=x2+(2-2m)x+m2在x≥0时为增函数,
∴$|PA{|}_{min}=\sqrt{g(0)}=\sqrt{{m}^{2}}=m$,此时P的横坐标为0;
(2)当m-1≥0即m≥1时,
g(x)=x2+(2-2m)x+m2(x≥0)在(0,m-1)上递减,在(m-1,+∞)上递增,
∴$|PA{|}_{min}=\sqrt{g(m-1)}$=$\sqrt{2m-1}$,此时P的横坐标为m-1.
综上所述,当m<1,点P与点A的距离的最小值为m,P的横坐标为0;当m≥1,点P与点A的距离的最小值为$\sqrt{2m-1}$,P的横坐标为m-1.
点评 本题考查抛物线的简单性质,考查二次函数在固定区间上的最值求法.在求二次函数在固定区间上的最值时,一定要注意分对称轴在区间左边,对称轴在区间右边以及对称轴在区间中间三种情况来讨论,此题是中档题.

练习册系列答案
相关题目
16.已知全集U={1,2,3,4,5,6,7},A={2,4,6},B={1,3,5,6,7},则A∩(∁UB)等于( )
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4} | D. | {2,5} |
14. 如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
 如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )
如图,四边形ABCD为矩形,AB=$\sqrt{3}$,BC=1,以A为圆心,1为半径作四分之一个圆弧DE,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
16.一套共7册的书计划每2年出一册,若各册书的出版年份数之和为14035,则出齐这套书的年份是( )
| A. | 2005 | B. | 2007 | C. | 2009 | D. | 2011 |
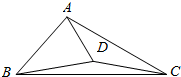 已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.
已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.