题目内容
11.设函数f(x)=x3+x,若0<θ≤$\frac{π}{2}$时,f(mcosθ)+f(1-m)>0恒成立,则实数m的取值范围是( )| A. | (-∞,1) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (1,+∞) |
分析 利用函数f(x)=x3+x是奇函数又是[0,$\frac{π}{2}$]上的增函数,把不等式转化求解.
解答 解:∵函数f(x)=x3+x是奇函数又是(0,$\frac{π}{2}$]上的增函数,
∴f(mcosθ)+f(1-m)>0恒成立,等价于f(mcosθ)>-f(1-m)
即f(mcosθ)>f(m-1)即mcosθ>m-1⇒m<$\frac{1}{1-cosθ}$,
又0<θ≤$\frac{π}{2}$时,0≤cosθ<1,
即有$\frac{1}{1-cosθ}$≥1,
∴m<1.
故选:A.
点评 考查函数的奇偶性单调性的综合运用以及三角函数的单调性的运用能力,属中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
2.某中学高一年级举办了一次科普知识竞赛,该竞赛分为预赛和决赛两个阶段.预赛为笔试,决赛为面试,现将所有参赛选手参加笔试的成绩(得分均为正数,满分100分)进行统计,制成如下频率分布表.
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
19.同时投掷两颗骰子,则两颗骰子向上的点数相同的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
16.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a1 $\overrightarrow{OA}$+a2011$\overrightarrow{OC}$,且A、B、C三点共线(O为该直线外一点),则S2011=( )
| A. | 2011 | B. | $\frac{2011}{2}$ | C. | 22011 | D. | 2-2011 |
 是定义在实数集
是定义在实数集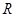 上的奇函数,且当
上的奇函数,且当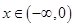 时,
时,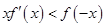 成立,若
成立,若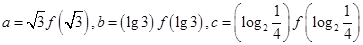 ,则
,则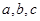 大小关系( )
大小关系( )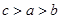 B.
B.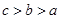
 D.
D.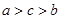
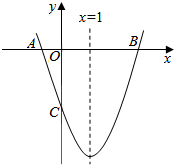 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.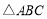 中,内角
中,内角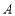 ,
,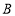 ,
,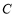 所对的边分别为
所对的边分别为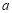 ,
,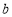 ,
,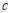 ,且
,且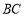 边上的高为
边上的高为 ,则
,则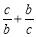 的最大值为( )
的最大值为( )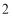 B.
B.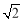
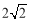 D.4
D.4