题目内容
已知函数f(x)=ax2-2x+1,g(x)=ln(x+1).
(1)求函数y=g(x)-x在[0,1]上的最小值;
(2)当a≥![]() 时,函数t(x)=f(x)+g(x)的图像记为曲线C,曲线C在点(0,1)处的切线为l,是否存在a使l与曲线C有且仅有一个公共点?若存在,求出所有a的值;否则,说明理由.
时,函数t(x)=f(x)+g(x)的图像记为曲线C,曲线C在点(0,1)处的切线为l,是否存在a使l与曲线C有且仅有一个公共点?若存在,求出所有a的值;否则,说明理由.
(3)当x≥0时,g(x)≥-![]() f(x)+
f(x)+![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
解析 (1)y′=![]() -1,因为0≤x≤1,所以y′≤0.
-1,因为0≤x≤1,所以y′≤0.
所以y=g(x)-x在[0,1]上单调递减.
当x=1时,y取最小值为ln2-1.
故y=g(x)-x在[0,1]的最小值为ln2-1.
(2)函数t(x)的定义域为(-1,+∞),t′(x)=2ax-2+![]() ,t′(0)=-1.
,t′(0)=-1.
所以在切点P(0,1)处的切线l的斜率为-1.
因此切线方程为y=-x+1.
因此切线l与曲线C有唯一的公共点,所以,方程ax2-x+ln(x+1)=0有![]() 且只有一个实数解.显然,x=0是方程的一个解.
且只有一个实数解.显然,x=0是方程的一个解.
令φ(x)=ax2-x+ln(x+1),则φ′(x)=2ax-1+![]() =
=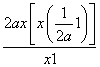 .
.
当a=![]() 时,φ′(x)=
时,φ′(x)=![]() ≥0,于是,φ(x)在(-1,+∞)上单调递增,即x=0是方程唯一的实数解.
≥0,于是,φ(x)在(-1,+∞)上单调递增,即x=0是方程唯一的实数解.
当a>![]() 时,由φ′(x)=0,得x1=0,x2=
时,由φ′(x)=0,得x1=0,x2=![]() -1∈(-1,0).
-1∈(-1,0).
在区间(-1,x2)上,φ′(x)>0,在区间(x2,0)上,φ′(x)<0.
所以,函数φ(x)在x2处有极大值φ(x2),且φ(x2)>φ(0)=0.
而当x→-1时,φ(x)→-∞,因此,φ(x)=0在(-1,x2)内也有一个解,矛盾.
综上,得a=![]() .
.
(3)令h(x)=g(x)-![]() =ln(x+1)+
=ln(x+1)+![]() ax2-x,
ax2-x,
h′(x)=![]() +ax-1=
+ax-1=![]() =
=![]() (x>-1).
(x>-1).
若a=0,当x∈[0,+∞)时,h′(x)≤0,则h(x)在[0,+∞)上单调递减,故h(x)≤h(0)=0,不合题意;
若a≥1,当x∈[0,+∞)时,h′(x)≥0,则h(x)在[0,+∞)上单调递增,故h(x)≥h(0)=0,符合题意;
若0<a<1,当x∈![]() 时,h′(x)≤0,则h(x)在
时,h′(x)≤0,则h(x)在![]() 单调递减,故h(
单调递减,故h(![]() )<h(0)=0,不合题意;
)<h(0)=0,不合题意;
若a<0,当x∈[0,+∞)时,h![]() ′(x)≤0,则h(x)在[0,+∞)单调递减,故h(1)<h(0)=0,不合题意.
′(x)≤0,则h(x)在[0,+∞)单调递减,故h(1)<h(0)=0,不合题意.
综上:a的取值范围是a≥1.

 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4. .
. (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值. )
)