题目内容
( (本小题满分13分)
已知函数f(x)=(a-1)x+aln(x-2),(a<1).
(1)讨论函数f(x)的单调性;
(2)设a<0时,对任意x1、x2∈(2,+∞),<-4恒成立,求a的取值范围.
.解:(1) ∵f′(x)=(a-1)+=(1分)
①a<0时,f′(x)=
∵-2=<0,∴0<<2,∴x>2时,f′(x)<0
∴f(x)在(2,+∞)上递减.(3分)
②a=0时,f(x)=-x,在(2,+∞)上递减.(4分)
③0<a<1时,>2
∴x∈(2, )时,f′(x)>0,f(x)在(2,)上递增;
当x∈(,+∞)时,f′(x)<0,f(x)在(,+∞)上递减;(6分)
∴综上所述,当a≤0时,f(x)在(2,+∞)上递减,
当0<a<1时,f(x)在(2,)上递增,在(,+∞)上递减.(7分)
(2)当a<0时,f(x)在(2,+∞)上递减;
不妨设任意x1,x2∈(2,+∞)且x1<x2
<-4可变为f(x1)-f(x2)>-4(x1-x2)
f(x1)+4x1>f(x2)+4x2
∴令g(x)=f(x)+4x,∴g(x)在(2,+∞)上递减
∴g′(x)<0在(2,+∞)上恒成立
∴a-1++4<0在(2,+∞)上恒成立.
a<-3+在(2,+∞)上恒成立
而-3<-3+<0,∴a≤-3.(13分)
【解析】略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
(本小题满分13分)
随机变量X的分布列如下表如示,若数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,则称随机变量X服从等比分布,记为Q(
为公比的等比数列,则称随机变量X服从等比分布,记为Q( ,
, ).现随机变量X∽Q(
).现随机变量X∽Q( ,2).
,2).
|
X |
1 |
2 |
… |
n |
|
|
|
|
… |
|
(Ⅰ)求n 的值并求随机变量X的数学期望EX;
(Ⅱ)一个盒子里装有标号为1,2,…,n且质地相同的标签若干张,从中任取1张标签所得的标号为随机变量X.现有放回的从中每次抽取一张,共抽取三次,求恰好2次取得标签的标号不大于3的概率.
 经过点
经过点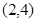 .
.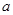 的值;(2)求
的值;(2)求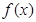 在[0,1]上的最大值与最小值.
在[0,1]上的最大值与最小值.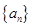 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,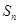 为
为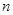 项和.
项和.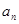 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列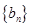 的通项公式及其前
的通项公式及其前 .
.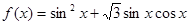

 的最小正周期和值域;
的最小正周期和值域; 的图象按向量
的图象按向量 平移后得到函数
平移后得到函数 的图
象,求函数
的图
象,求函数 是二次函数,不等式
是二次函数,不等式 的解集是(0,5),且
的解集是(0,5),且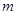 ,使得方程
,使得方程 在区间
在区间 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出

