题目内容
(12分)已知函数f(x)＝
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
【答案】
f(x)＝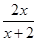
，f[f(－4)]＝
.
【解析】本试题主要是考查了函数的 解析式的求解和运用。先分析f(x)＝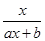
且f(2)＝1，∴2＝2a＋b.
又∵方程f(x)＝x有唯一实数解．
∴ax2＋(b－1)x＝0(a≠0)有唯一实数解．
故(b－1)2－4a×0＝0，即b＝1，进而得到a的值，得到解析式，并求解函数值。
解：∵f(x)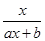＝且f(2)＝1，∴2＝2a＋b.
又∵方程f(x)＝x有唯一实数解．
∴ax2＋(b－1)x＝0(a≠0)有唯一实数解．
故(b－1)2－4a×0＝0，即b＝1，又上式2a＋b＝2，可得：
a＝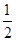
，从而f(x)＝
＝，
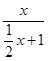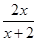∴f(－4)＝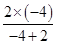
＝4，f(4)＝
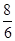＝，即f[f(－4)]＝.
练习册系列答案
相关题目
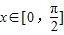，求f（x）的最大值，最小值．
（x∈R），Ｐ1（ｘ1，ｙ1），Ｐ2（ｘ2，ｙ2）是函数ｙ＝ｆ(x)图像上两点，且线段Ｐ1Ｐ2中点Ｐ的横坐标为
。
｝的通项公式为
)(ｍ∈Ｎ
，ｎ＝１,２,３,…,ｍ），求数列｛
； （5分）
＜
横成立，求实数a的取值范围。（3分）
)=
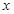,当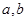
的值及函数f(
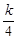f(
，问