题目内容
(本小题满分l2分)
已知函数f(x)=a-
(1)求证:函数y=f(x)在(0,+∞)上是增函数;
(2)若f(x)<2x在(1,+∞)上恒成立,求实数a的取值范围.
【答案】
解:(1)证明:当x∈(0,+∞)时,f(x)=a-,
设0<x1<x2,则x1x2>0,x2-x1>0.
f(x1)-f(x2)=(a-)-(a-)=-
=<0.∴f(x1)<f(x2),即f(x)在(0,+∞)上是增函数.
(2)由题意a-<2x在(1,+∞)上恒成立,
设h(x)=2x+,则a<h(x)在(1,+∞)上恒成立.
可证h(x)在(1,+∞)上单调递增.故a≤h(1),即a≤3,
∴a的取值范围为(-∞,3].
【解析】略

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线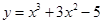 相切的直线方程.
相切的直线方程.