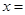题目内容
椭圆
+
=1的右焦点为F,P是椭圆上一点,点M满足|
|=1,
•
=0,则|MP|的最小值为( )
| x2 |
| 25 |
| y2 |
| 16 |
| MF |
| MF |
| MP |
| A.3 | B.
| C.2 | D.
|
依题意得a=5,b=4,
故c=
=3,∴F(3,0),
由
•
=0可得MF⊥MP,
故|MP|=
=
,
要使|MP|最小,则需|PF|最小,
当P为右顶点时,|PF|取最小值a-c=2,
故|MP|的最小值为
,
故选B
故c=
| a2-b2 |
由
| MF |
| MP |
故|MP|=
|
|
|
|
要使|MP|最小,则需|PF|最小,
当P为右顶点时,|PF|取最小值a-c=2,
故|MP|的最小值为
| 3 |
故选B

练习册系列答案
相关题目
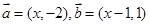 互相垂直,则
互相垂直,则