题目内容
已知函数f(x)=sin2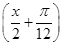 +
+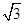 sin
sin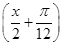
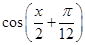 -
-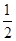 .
.
(1)在△ABC中,若sin C=2sin A,B为锐角且有f(B)=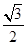 ,求角A,B,C;
,求角A,B,C;
(2)若f(x)(x>0)的图象与直线y=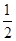 交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.
交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.
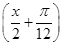 +
+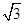 sin
sin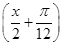
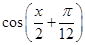 -
-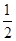 .
.(1)在△ABC中,若sin C=2sin A,B为锐角且有f(B)=
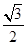 ,求角A,B,C;
,求角A,B,C;(2)若f(x)(x>0)的图象与直线y=
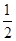 交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.
交点的横坐标由小到大依次是x1,x2,…,xn,求数列{xn}的前2n项和,n∈N*.(1)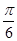 (2)(2n2-n)π.
(2)(2n2-n)π.
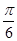 (2)(2n2-n)π.
(2)(2n2-n)π.(1)因为f(x)=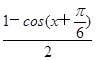 +
+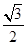 sin
sin 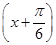 -
-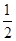 =
=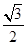 sin
sin 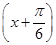 -
-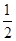 cos
cos 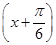 =sin
=sin 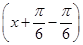 =sin x,
=sin x,
又因为f(B)=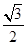 ,故sin B=
,故sin B=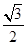 .又B为锐角,所以B=
.又B为锐角,所以B=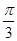 .
.
由sin C=2sin A,得c=2a,所以b2=a2+4a2-2a·2acos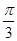 =3a2.所以c2=a2+b2.所以△ABC为直角三角形,C=
=3a2.所以c2=a2+b2.所以△ABC为直角三角形,C=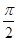 ,A=
,A=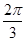 -
-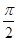 =
=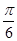 .
.
(2)由正弦曲线的对称性、周期性,可知
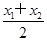 =
=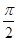 ,
,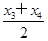 =2π+
=2π+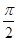 ,…,
,…,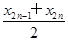 =2(n-1)π+
=2(n-1)π+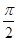 ,
,
所以x1+x2+…+x2n-1+x2n=π+5π+9π+…+(4n-3)π=nπ+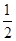 n(n-1)·4π=(2n2-n)π.
n(n-1)·4π=(2n2-n)π.
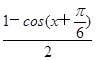 +
+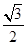 sin
sin 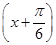 -
-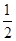 =
=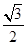 sin
sin 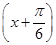 -
-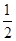 cos
cos 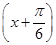 =sin
=sin 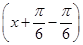 =sin x,
=sin x,又因为f(B)=
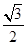 ,故sin B=
,故sin B=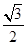 .又B为锐角,所以B=
.又B为锐角,所以B=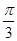 .
.由sin C=2sin A,得c=2a,所以b2=a2+4a2-2a·2acos
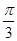 =3a2.所以c2=a2+b2.所以△ABC为直角三角形,C=
=3a2.所以c2=a2+b2.所以△ABC为直角三角形,C=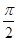 ,A=
,A=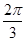 -
-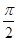 =
=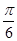 .
.(2)由正弦曲线的对称性、周期性,可知
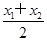 =
=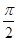 ,
,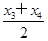 =2π+
=2π+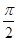 ,…,
,…,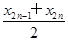 =2(n-1)π+
=2(n-1)π+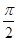 ,
,所以x1+x2+…+x2n-1+x2n=π+5π+9π+…+(4n-3)π=nπ+
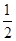 n(n-1)·4π=(2n2-n)π.
n(n-1)·4π=(2n2-n)π.
练习册系列答案
相关题目
 ,
, ,函数
,函数 ,
,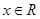 .
.
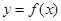 的图像的对称中心坐标;
的图像的对称中心坐标; 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 上的图像.
上的图像. sinxcosx-2cos2x+l.
sinxcosx-2cos2x+l.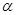 ∈(0,
∈(0, ),且f(
),且f(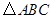 中,角
中,角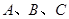 所对的边分别为
所对的边分别为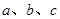 ,已知
,已知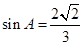 ,
,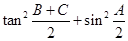 的值;
的值;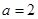 ,
,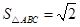 ,求
,求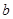 的值.
的值. ,使
,使 ; ②函数
; ②函数 是偶函数;
是偶函数;  是函数
是函数 的一条对称轴的方程;
的一条对称轴的方程; 是第一象限的角,且
是第一象限的角,且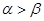 ,则
,则 .
.

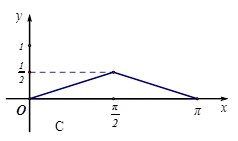
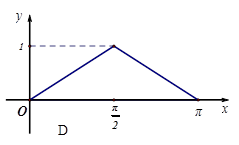
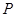 在半径为
在半径为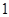 的半圆上运动,
的半圆上运动,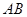 是直径,当
是直径,当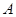 到
到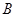 运动时,点
运动时,点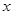 与
与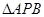 的面积
的面积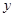 的函数
的函数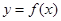 的图像是下图中的( )
的图像是下图中的( )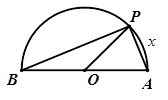
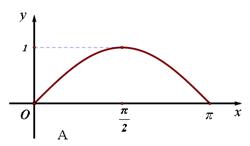
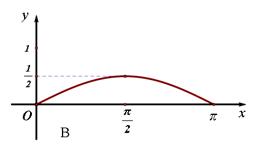
 sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)=
sinωx,0),n=(cosωx,-sinωx)(ω>0),在函数f(x)= ,且当x∈[0,
,且当x∈[0, ]时,f(x)的最大值为1.
]时,f(x)的最大值为1. 有实根,则实数
有实根,则实数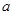 的取值范围为
的取值范围为