题目内容
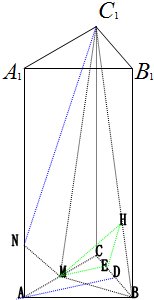
如图，在正三棱柱ABC-A1 B1 C1中，AA1=4，AB=2，M是AC的中点，点N在AA1上，AN=| 1 |
| 4 |
（1）求BC1与侧面AC C1 A1所成角的正弦值；
（2）证明：MN⊥B C1；
（3）求二面角C-C1B-M的平面角的正弦值，若在△A1B1C1中，
| C1E |
| 1 |
| 3 |
| EA1 |
| C1F |
| 1 |
| 4 |
| FB1 |
| C1H |
| C1A1 |
| C1B1 |
分析：（1）由等边三角形ABC的性质可得BM⊥AC，由正三棱柱的性质可得 C1 C⊥BM，利用线面垂直的判定定理可得BM⊥侧面ACC1A1，于是∠BC1M是所求的线面角；
（2）利用勾股定理和逆定理即可证明MN⊥MC1，再利用（1）可得BM⊥MN，利用线面垂直的判定定理即可证明；
（3）作AD⊥BC，ME‖AD，可得ME⊥BC．作EH⊥B C1，连接MH，利用正三棱柱的性质和三垂线定理得 B C1⊥MH，∴∠MHE为二面角C-C1B-M的平面角．
利用向量共线定理找出
与
的关系，再利用向量的运算法则
=
+
及已知条件即可得出．
（2）利用勾股定理和逆定理即可证明MN⊥MC1，再利用（1）可得BM⊥MN，利用线面垂直的判定定理即可证明；
（3）作AD⊥BC，ME‖AD，可得ME⊥BC．作EH⊥B C1，连接MH，利用正三棱柱的性质和三垂线定理得 B C1⊥MH，∴∠MHE为二面角C-C1B-M的平面角．
利用向量共线定理找出
| EH |
| EB1 |
| C1H |
| C1E |
| EH |
解答：（1）解：在等边三角形ABC中，M为AC中点，BM⊥AC，
在正三棱柱中，C1 C⊥面ABC，BM?面ABC，∴C1 C⊥BM，
又 C1 C∩AC=C，BM?面ABC，
则BM⊥面 A1 C1CA，
∠M C1 B为 B C1与面 A1 C1CA所成角．
在 Rt△C1CB中，B C1=2
，在等边三角形ABC中，BM=
，
则在 Rt△M C1 B中，sin∠M C1 B=
=
．
（2）连接 N C1，在 Rt△AMN中，由勾股定理可得MN2=AM2+AN2=12+(
)2=
，
同理在 Rt△M C1 C中，C1M =
，在 Rt△A1 C1 N中，C1N =
，
∴(MN)2+ (M C1)2=(C1N )2，则NM⊥M C1，
又BM⊥面 A1 C1CA，MN?面 A1 C1CA，则BM⊥MN，
又 M C1∩MB=M，∴MN⊥面 M C1 B，
又 B C1?面 M C1 B，则MN⊥B C1．
（3）作AD⊥BC，ME‖AD，此时由于M为AC中点，则DE=EC，ME=
AD=
，且ME⊥BC，
在正三棱柱中，C1 C⊥面ABC，ME?面ABC，则 C1 C⊥ME，BC∩C1C=C，BC，C1 C均?面BC C1，ME⊥面BC C1，
作EH⊥B C1，连接MH，由三垂线定理得 B C1⊥MH，∴∠MHE为二面角C-C1B-M的平面角．
在△MB C1中，由
MB×M C1=
B C1×MH ，即
×
×
=
×2
×MH，MH=
，
在 Rt△MEH中，sin∠MHE=
=
．
设
=m
=m(
+
=m(-
+
)，
=n
=n(
+
)=n(-
+
)．
∵
+
=
=
．
∴
=m(-
+
)+n(-
+
)，
化为(
+
-n)
+(
-m)
=
，
∴
，解得
．
∴
=
+
=
+
=
+
(
+
)=
+
(-
+
)=
+
．
∵
=x
+y
，
∴x+y=
．
在正三棱柱中，C1 C⊥面ABC，BM?面ABC，∴C1 C⊥BM，
又 C1 C∩AC=C，BM?面ABC，
则BM⊥面 A1 C1CA，
∠M C1 B为 B C1与面 A1 C1CA所成角．
在 Rt△C1CB中，B C1=2
| 5 |
| 3 |
则在 Rt△M C1 B中，sin∠M C1 B=
| BM |
| B C1 |
| ||
2
|
（2）连接 N C1，在 Rt△AMN中，由勾股定理可得MN2=AM2+AN2=12+(
| 1 |
| 4 |
| 17 |
| 16 |
同理在 Rt△M C1 C中，C1M =
| 17 |
| 17 |
| 4 |
∴(MN)2+ (M C1)2=(C1N )2，则NM⊥M C1，
又BM⊥面 A1 C1CA，MN?面 A1 C1CA，则BM⊥MN，
又 M C1∩MB=M，∴MN⊥面 M C1 B，
又 B C1?面 M C1 B，则MN⊥B C1．
（3）作AD⊥BC，ME‖AD，此时由于M为AC中点，则DE=EC，ME=
| 1 |
| 2 |
| ||
| 2 |
在正三棱柱中，C1 C⊥面ABC，ME?面ABC，则 C1 C⊥ME，BC∩C1C=C，BC，C1 C均?面BC C1，ME⊥面BC C1，
作EH⊥B C1，连接MH，由三垂线定理得 B C1⊥MH，∴∠MHE为二面角C-C1B-M的平面角．
在△MB C1中，由
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 17 |
| 1 |
| 2 |
| 5 |
| ||||
2
|
在 Rt△MEH中，sin∠MHE=
| ME |
| MH |
| ||
| 17 |
设
| EH |
| EB1 |
| EC1 |
| C1B1) |
| 1 |
| 4 |
| C1A1 |
| C1B1 |
| HA1 |
| FA1 |
| FC1 |
| C1A1 |
| 1 |
| 5 |
| C1B1 |
| C1A1 |
∵
| EH |
| HA1 |
| EA1 |
| 3 |
| 4 |
| C1A1 |
∴
| 3 |
| 4 |
| C1A1 |
| 1 |
| 4 |
| C1A1 |
| C1B1 |
| 1 |
| 5 |
| C1B1 |
| C1A1 |
化为(
| 3 |
| 4 |
| m |
| 4 |
| C1A1 |
| n |
| 5 |
| C1B1 |
| 0 |
∴
|
|
∴
| C1H |
| C1E |
| EH |
| 1 |
| 4 |
| C1A1 |
| 3 |
| 19 |
| EB1 |
| 1 |
| 4 |
| C1A1 |
| 3 |
| 19 |
| EC1 |
| C1B1 |
| 1 |
| 4 |
| C1A1 |
| 3 |
| 19 |
| 1 |
| 4 |
| C1A1 |
| C1B1 |
| 4 |
| 19 |
| C1A1 |
| 3 |
| 19 |
| C1B1 |
∵
| C1H |
| C1A1 |
| C1B1 |
∴x+y=
| 7 |
| 19 |
点评：熟练掌握等边三角形的性质、正三棱柱的性质、线面垂直的判定定理、线面角的定义、勾股定理和逆定理、三垂线定理、二面角定义和作法、向量共线定理、向量的运算法则是解题的关键．
练习册系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AB=1，若二面角C-AB-C1的大小为60°，则点C到平面C1AB的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
如图，在正三棱柱ABC-A1B1C1中，D、E、G分别是AB、BB1、AC1的中点，AB=BB1=2．
如图，在正三棱柱ABC-A1B1C1中，AA1=4，AB=2，M是AC的中点，点N在AA1上，
（2012•马鞍山二模）如图，在正三棱柱ABC一DEF中，AB=2，AD=1，P是CF的延长线上一点，过A、B、P三点的平面交FD于M，交EF于N．