题目内容
【题目】随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润． （Ⅰ）视x分布在各区间内的频率为相应的概率，求P（x≥120）
（Ⅱ）将T表示为x的函数，求出该函数表达式；
（Ⅲ）在频率分布直方图的市场需求量分组中，以各组的区间中点值（组中值）代表该组的各个值，并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率（例如x∈[100，110），则取x=105，且x=105的概率等于市场需求量落入100，110）的频率），求T的分布列及数学期望E（T）．
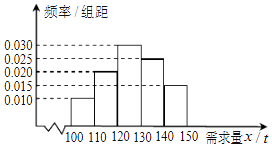
【答案】解：（Ⅰ）根据频率分布直方图及两两互斥事件概率的可加性得P（x≥120）=P（120≤x＜130）+P（130≤x＜140）+P（140≤x≤150）=0.030×10+0.025×10+0.015×10=0.7． （Ⅱ）当x∈[100，130）时，T=0.5x﹣0.3（130﹣x）=0.8x﹣39；
当x∈[130，150]时，T=0.5×130=65．
∴T= 
．
（Ⅲ）由题意及（Ⅱ）可得：
当x∈[100，110）时，T=0.8×105﹣39=45，P（T=45）=0.010×10=0.1；
当x∈[110，120）时，T=0.8×115﹣39=53，P（T=53）=0.020×10=0.2；
当x∈[120，130）时，T=0.8×125﹣39=61，P（T=61）=0.030×10=0.3；
当x∈[130，150）时，T=65，P（T=65）=（0.025+0.015）×10=0.4．
所以T的分布列为
T | 45 | 53 | 61 | 65 |
P | 0.1 | 0.2 | 0.3 | 0.4 |
所以，E（T）=45×0.1+53×0.2+61×0.3+65×0.4=59.4（万元）
【解析】（Ⅰ）根据频率分布直方图及两两互斥事件概率的可加性得P（x≥120）=P（120≤x＜130）+P（130≤x＜140）+P（140≤x≤150）．（Ⅱ）当x∈[100，130）时，T=0.5x﹣0.3（130﹣x）=0.8x﹣39；当x∈[130，150]时，T=0.5×130，即可得出．（Ⅲ）由题意及（Ⅱ）可得：当x∈[100，110）时，T=0.8×105﹣39，P（T=45）=0.010×10；当x∈[110，120）时，T=0.8×115﹣39，P（T=53）=0.020×10；当x∈[120，130）时，T=0.8×125﹣39，P（T=61）=0.030×10；当x∈[130，150）时，T=65，P（T=65）=（0.025+0.015）×10．即可得出T的分布列及其数学期望．
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本，需要知道在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．
