题目内容
【题目】已知椭圆C: ![]() 的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
(1)求椭圆C的方程;
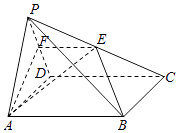
(2)直线l:x=my+3(m≠0)交椭圆C于M,N两点,设点N关于x轴的对称点为N1(点N1与点M不重合),且直线N1M与x轴的交于点P,试问△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
【答案】
(1)解:∵椭圆C的左顶点A在圆x2+y2=12上,∴ ![]()
又∵椭圆的一个焦点为F(3,0),∴c=3∴b2=a2﹣c2=3
∴椭圆C的方程为 ![]()
(2)解:设M(x1,y1),N(x2,y2),则直线与椭圆C方程联立 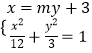
化简并整理得(m2+4)y2+6my﹣3=0,
∴ ![]() ,
, ![]()
由题设知N1(x2,﹣y2)∴直线NM的方程为 ![]()
令y=0得 ![]() =
= 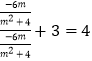 ,
,
∴点P(4,0)
![]() =
= ![]()
= 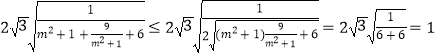 (当且仅当
(当且仅当 ![]() 即
即 ![]() 时等号成立),
时等号成立),
∴△PMN的面积存在最大值,最大值为1
【解析】(1)由椭圆C的左顶点A在圆x2+y2=12上,求得a,由椭圆的一个焦点得c=3,由b2=a2﹣c2得b,即可.(2)由题意,N1(x2 , ﹣y2),可得直线NM的方程,令y=0,可得点P的坐标为(4,0). 利用△PMN的面积为S= ![]() |PF||y1﹣y2|,化简了基本不等式的性质即可得出.
|PF||y1﹣y2|,化简了基本不等式的性质即可得出.

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
不常喝 | 常喝 | 合计 | |
肥胖 | x | y | 50 |
不肥胖 | 40 | 10 | 50 |
合计 | A | B | 100 |
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为 ![]()
(1)求2×2列联表中的数据x,y,A,B的值;
(2)根据列联表中的数据绘制肥胖率的条形统计图,并判断常喝碳酸饮料是否影响肥胖?
(3)是否有99.9%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |