题目内容
【题目】已知数列{an}中, ![]() 的对称轴为
的对称轴为 ![]() .
.
(1)试证明{2nan}是等差数列,并求{an}的通项公式;
(2)设{an}的前n项和为Sn , 求Sn .
【答案】
(1)证明:∵ ![]() 的对称轴为
的对称轴为 ![]() .
.
∴an≠0, ![]() =
= ![]() ,化为:2n+1an+1﹣2nan=2,
,化为:2n+1an+1﹣2nan=2,
∴{2nan}是等差数列,首项为2,公差为2.
∴2nan=2+2(n﹣1)=2n.
(2)解:由(1)可得:an= ![]() .
.
∴Sn=1+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,
![]() =
= ![]() +…+
+…+ ![]() +
+ ![]() ,
,
∴ ![]() =1+
=1+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() =2﹣
=2﹣ ![]() ,
,
∴Sn=4﹣ ![]()
【解析】(1)由于 ![]() 的对称轴为
的对称轴为 ![]() .可得an≠0,
.可得an≠0, ![]() =
= ![]() ,化简整理即可证明.()由(1)可得:an=
,化简整理即可证明.()由(1)可得:an= ![]() .利用“错位相减法”与等比数列的前n项和公式即可得出.
.利用“错位相减法”与等比数列的前n项和公式即可得出.
【考点精析】利用等差数列的通项公式(及其变式)和数列的前n项和对题目进行判断即可得到答案,需要熟知通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系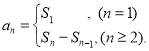 .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目