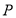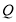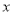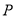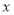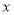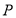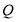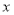题目内容

下列函数图象关于原点对称的有（ ）

①；②；

③④.

A．①② B．①③ C．②③ D．②④

 

D

【解析】

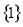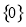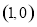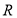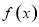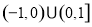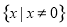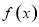试题分析：在函数①的定义域为，值域为，所以函数图像为只有一个点，不关于原点对称；在函数②定义域为，且函数为奇函数，所以其图像关于原点对称；在函数③的定义域为不关于原点对称；函数④的定义域为，且函数为奇函数，所以其图像关于原点对称.所以正确答案为D.

考点：1.奇函数；2.函数定义域.

 

练习册系列答案
相关题目

已知，则由小到大的顺序是　　　　　．

 

设是整数集的一个非空子集，对于，若，且，则称是的一个“孤立元”。给定集合，在由的三个元素构成的所有集合中，不含“孤立元”的集合个数为 ．

 

已知集合与分别是函数的定义域与值域.

（1）求集合；

（2）当时，求实数的取值范围．

 

定义域为R的函数，若关于的方程有3个不同实数解，且，则下列说法错误的是（ ）

A． B．

C． D．

 

若非零函数对任意实数均有，且当时

（1）求证：；

（2）求证：为R上的减函数；

（3）当时， 对恒有，求实数的取值范围.

 

函数在区间上是递减的，则实数k的取值范围为 ．

 

已知.

（1）求的值；

（2）求的值.

 

现有A，B两个投资项目，投资两项目所获得利润分别是和（万元），它们与投入资金(万元)的关系依次是：其中与平方根成正比，且当为4（万元）时为1（万元），又与成正比，当为4（万元）时也是1（万元）；某人甲有3万元资金投资.

（1）分别求出，与的函数关系式；

（2）请帮甲设计一个合理的投资方案，使其获利最大，并求出最大利润是多少？

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网