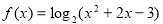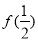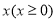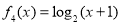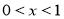题目内容
若非零函数 对任意实数
对任意实数 均有
均有 ,且当
,且当 时
时
(1)求证: ;
;
(2)求证: 为R上的减函数;
为R上的减函数;
(3)当 时, 对
时, 对 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围.
(1)证法一: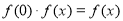 即
即 又
又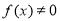
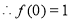
当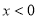 时,
时,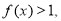
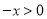
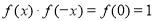 则
则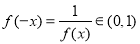
故对于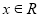 恒有
恒有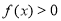
证法二: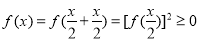
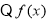 为非零函数
为非零函数 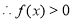
(2)证明:令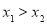 且
且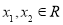
有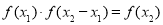 , 又
, 又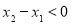 即
即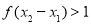
故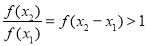 又
又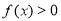
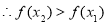
故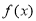 为R上的减函数
为R上的减函数
(3)实数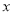 的取值范围为
的取值范围为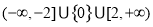
【解析】
试题分析:(1)由题意可取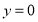 代入等式
代入等式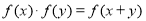 ,得出关于
,得出关于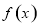 的方程,因为
的方程,因为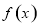 为非零函数,故
为非零函数,故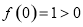 ,再令
,再令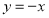 代入等式,可证
代入等式,可证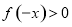 ,从而证明当
,从而证明当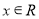 时,有
时,有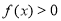 ;(2)着眼于减函数的定义,利用条件当
;(2)着眼于减函数的定义,利用条件当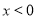 时,有
时,有 ,根据等式
,根据等式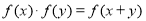 ,令
,令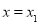 ,
,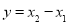 ,可得
,可得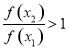 ,从而可证该函数为减函数.(3)根据
,从而可证该函数为减函数.(3)根据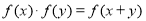 ,由条件
,由条件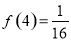 可求得
可求得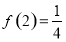 ,将
,将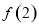 替换不等式中的
替换不等式中的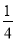 ,再根据函数的单调性可得
,再根据函数的单调性可得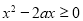 ,结合
,结合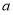 的范围,从而得解.
的范围,从而得解.
试题解析:(1)证法一: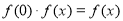 即
即 又
又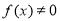
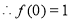
当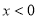 时,
时,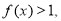
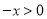
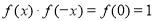 则
则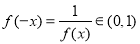
故对于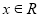 恒有
恒有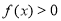 4分
4分
证法二: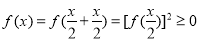
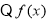 为非零函数
为非零函数 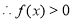
(2)令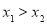 且
且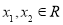
有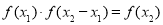 , 又
, 又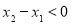 即
即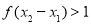
故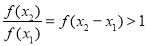 又
又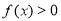
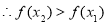
故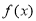 为R上的减函数 8分
为R上的减函数 8分
(3)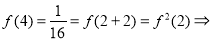 故
故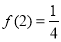 , 10分
, 10分
则原不等式可变形为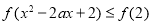
依题意有 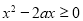 对
对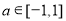 恒成立
恒成立
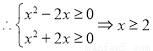 或
或 或
或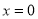
故实数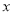 的取值范围为
的取值范围为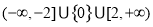 14分
14分
考点:1.函数的概念;2.函数的单调性;3.二次函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目