题目内容
【题目】在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ![]() ,M为AB的中点.
,M为AB的中点. 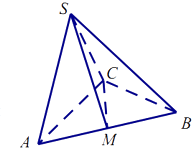
(1)求证:AC⊥SB;
(2)求二面角S﹣CM﹣A的平面角的余弦值.
【答案】
(1)证明:取AC的中点O,连结OS、OB,
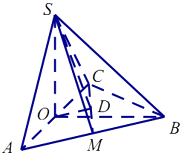
∵SA=SC,∴AC⊥OS,
∵BA=BC,∴AC⊥OB,
又OS,OB平面OSB,OS∩OB=O,
∴AC⊥平面OSB,
∴AC⊥SB
(2)解:∵平面SAC⊥平面ABC,SO⊥AC,
∴由面面垂直性质定理,得SO⊥面ABC,
过O作OD⊥CM于D,连结SD,
由三垂线定理,得SD⊥CM,
∴∠SDO是二面角N﹣CM﹣B的平面角,
又SO=2 ![]() ,OD=1,∴SD=
,OD=1,∴SD= ![]() =3,
=3,
∴cos∠SDO= ![]() ,
,
∴二面角S﹣CM﹣A的平面角的余弦值为 ![]()
【解析】(1)取AC的中点O,连结OS、OB,由已知推导出AC⊥OS,AC⊥OB,由此能证明AC⊥SB.(2)平面SAC⊥平面ABC,SO⊥AC,从而SO⊥面ABC,过O作OD⊥CM于D,连结SD,则∠SDO是二面角N﹣CM﹣B的平面角,由此能求出二面角S﹣CM﹣A的平面角的余弦值.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.

练习册系列答案
相关题目