题目内容
【题目】数列{an}是公差d不为0的等差数列,a1=2,Sn为其前n项和.
(1)当a3=6时,若a1 , a3 , ![]() ,
, ![]() …,
…, ![]() 成等比数列(其中3<n1<n2<…<nk),求nk的表达式;
成等比数列(其中3<n1<n2<…<nk),求nk的表达式;
(2)是否存在合适的公差d,使得{an}的任意前3n项中,前n项的和与后n项的和的比值等于定常数?求出d,若不存在,说明理由.
【答案】
(1)解:数列{an}的公差d= ![]() =
= ![]() =2.
=2.
∴an=2+2(n﹣1)=2n,
另一方面,a1,a3, ![]() ,
, ![]() …,
…, ![]() 成等比数列(其中3<n1<n2<…<nk),
成等比数列(其中3<n1<n2<…<nk),
∴q= ![]() =3.
=3.
∴ ![]() ═a13k+2﹣1=2nk,
═a13k+2﹣1=2nk,
∴nk=3k+1.
(2)解:等差数列{an}中,Sn=na1+ ![]() =
= ![]() n2+
n2+ ![]() n,
n,
S3n﹣S2n= ![]() ﹣
﹣ ![]() =
= ![]() n2+
n2+ ![]() ,
,
令S3n﹣S2n=λSn,则 ![]() n2+
n2+ ![]() =λ[
=λ[ ![]() n2+
n2+ ![]() n],
n],
∴ 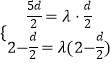 ,解得
,解得 ![]() 或
或 ![]() (舍去).
(舍去).
∴d=4,满足题意,且定 常数为5
【解析】(1)数列{an}的公差d= ![]() ,可得:an=2n.另一方面,a1 , a3 ,
,可得:an=2n.另一方面,a1 , a3 , ![]() ,
, ![]() …,
…, ![]() 成等比数列(其中3<n1<n2<…<nk),可得q=
成等比数列(其中3<n1<n2<…<nk),可得q= ![]() .利用等比数列的通项公式即可得出.(2)等差数列{an}中,Sn=
.利用等比数列的通项公式即可得出.(2)等差数列{an}中,Sn= ![]() n2+
n2+ ![]() n,可得S3n﹣S2n , 令S3n﹣S2n=λSn , 解出即可得出.
n,可得S3n﹣S2n , 令S3n﹣S2n=λSn , 解出即可得出.
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系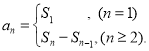 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目