题目内容
【题目】已知点P是圆F1：（x+1）2+y2=16上任意一点（F1是圆心），点F2与点F1关于原点对称．线段PF2的中垂线m分别与PF1、PF2交于M、N两点．
（1）求点M的轨迹C的方程；
（2）直线l经过F2 ， 与抛物线y2=4x交于A1 ， A2两点，与C交于B1 ， B2两点．当以B1B2为直径的圆经过F1时，求|A1A2|．
【答案】
（1）解：由题意得，F1（﹣1，0），F2（1，0），圆F1的半径为4，且|MF2|=|MP|，
从而|MF1|+|MF2|=|MF1|+|MP|=|PF1|=4＞|F1F2|，）
∴点M的轨迹是以F1，F2为焦点的椭圆，
其中长轴2a=4，得到a=2，焦距2c=2，
则短半轴b= 
，
椭圆方程为： 
（2）解：当直线l 与x轴垂直时，B1（1， 
），B2（1，﹣ ），又F1（﹣1，0），
此时 
，所以以B1B2为直径的圆不经过F1．不满足条件．
当直线l 不与x轴垂直时，设L：y=k（x﹣1）
由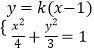 
即（3+4k2）x2﹣8k2x+4k2﹣12=0，
因为焦点在椭圆内部，所以恒有两个交点．
设B1（x1，y1），B2（x2，y2），则：x1+x2= 
，x1x2= 
，
因为以B1B2为直径的圆经过F1，所以 
，又F1（﹣1，0）
所以（﹣1﹣x1）（﹣1﹣x2）+y1y2=0，即（1+k2）x1x2+（1﹣k2）（x1+x2）+1+k2=0
所以解得k2= 
，
由 
得k2x2﹣（2k2+4）x+k2=0
因为直线l 与抛物线有两个交点，所以k≠0，
设A1（x3，y3），A2（x4，y4），则：x3+x4= 
=2+ 
，x3x4=1
所以|A1A2|=x3+x4+p=2+ +2= 
．
【解析】（1）先确定F1、F2的坐标，再根据线段PF2的中垂线与与PF1、PF2交于M点，结合椭圆的定义，可得点M的轨迹是以F1、F2为焦点的椭圆，从而可得点M的轨迹C的方程；（2）当直线l与x轴垂直时，B1（1， ），B2（1，﹣ ），不满足条件，当直线l不与x轴垂直时，设直线l的方程为：y=k（x﹣1），由 
，得（3+4k2）x2﹣8k2x+4k2﹣12=0，由此利用根的判别式、韦达定理、圆的性质、弦长公式能求出|A1A2|．
