题目内容
【题目】已知p:x2﹣6x+5≤0,q:x2﹣2x+1﹣m2≤0(m>0).
(1)若m=2,且p∧q为真,求实数x的取值范围;
(2)若p是q充分不必要条件,求实数m的取值范围.
【答案】
(1)解:由x2﹣6x+5≤0,得1≤x≤5,
∴p:1≤x≤5;
当m=2时,q:﹣1≤x≤3.
若p∧q为真,p,q同时为真命题.,
则 ![]() ,即1≤x≤3
,即1≤x≤3
(2)解:由x2﹣2x+1﹣m2≤0,得q:1﹣m≤x≤1+m.
∵p是q充分不必要条件,
∴[1,5][1﹣m,1+m],
∴ 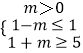 ,解得m≥4.
,解得m≥4.
∴实数m的取值范围为m≥4
【解析】(1)分别求解一元二次不等式化简p,q,然后利用p∧q为真,取交集求得实数x的取值范围;(2)求解一元二次不等式化简q,结合p是q充分不必要条件,可得[1,5][1﹣m,1+m],转化为关于m的不等式组得答案.
【考点精析】掌握复合命题的真假是解答本题的根本,需要知道“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目