题目内容
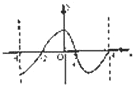
设函数f(x)的定义域为[-4,4],其图象如图,那么不等式
≤0的解集为______.
| f(x) |
| sinx |

不等式
≤0的解集即[-4,4]上f(x)与sinx异号的区间.
由函数图象可知:当f(x)≤0时,-4≤x≤-2,或1≤x≤4;
当f(x)≥0时,-2≤x≤1;
而sinx中的x∈[-4,4],当sinx>0时,x∈[-4,-π)∪(0,π);
当sinx<0时,x∈(-π,0)∪(π,4].
则
≤0,等价于
或
.
即 x∈[-4,-π)∪[-2,0)∪[1,π)∪{4},
故所求不等式的解集为[-4,-π)∪[-2,0)∪[1,π)∪{4}.
故答案为:[-4,-π)∪[-2,0)∪[1,π)∪{4}.
| f(x) |
| sinx |
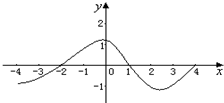
由函数图象可知:当f(x)≤0时,-4≤x≤-2,或1≤x≤4;
当f(x)≥0时,-2≤x≤1;
而sinx中的x∈[-4,4],当sinx>0时,x∈[-4,-π)∪(0,π);
当sinx<0时,x∈(-π,0)∪(π,4].
则
| f(x) |
| sinx |
|
|
即 x∈[-4,-π)∪[-2,0)∪[1,π)∪{4},
故所求不等式的解集为[-4,-π)∪[-2,0)∪[1,π)∪{4}.
故答案为:[-4,-π)∪[-2,0)∪[1,π)∪{4}.


练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
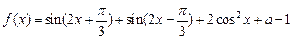 (
(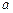 为常数),若函数
为常数),若函数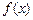 的最大值为
的最大值为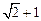 .(1)求实数
.(1)求实数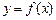 的图象向左平移
的图象向左平移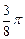 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数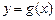 的图象,求函数
的图象,求函数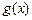 的单调递减区间.
的单调递减区间.




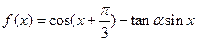 ,且
,且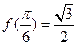 。
。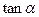 的值;(2)当
的值;(2)当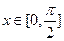 时,求函数
时,求函数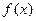 的值域。
的值域。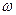 x+
x+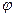 )(
)(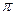
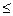
 ,且
,且 ,
, 为常数,
为常数, 的最小值是9,则
的最小值是9,则 ( )
( )