题目内容
【题目】已知函数![]() ,
,![]() 都在
都在![]() 处取得最小值.
处取得最小值.
(1)求![]() 的值;
的值;
(2)设函数![]() ,
,![]() 的极值点之和落在区间
的极值点之和落在区间![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .
.
(2)![]() .
.
【解析】分析:(1)先求![]() ,再求
,再求![]() ,列式可得导函数变化规律,确定单调性,得到最小值取法,即得
,列式可得导函数变化规律,确定单调性,得到最小值取法,即得![]() ,再根据
,再根据![]() 在
在![]() 处取得最小值得a,最后求
处取得最小值得a,最后求![]() 的值;(2)求
的值;(2)求![]() 导数,再求导函数的导数,根据导函数单调性以及零点存在定理得确定零点个数及其范围,最后确定极值点之和范围,进而得到k的值.
导数,再求导函数的导数,根据导函数单调性以及零点存在定理得确定零点个数及其范围,最后确定极值点之和范围,进而得到k的值.
详解:(1)![]() ,令
,令![]() 得
得![]() ,则
,则![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
| - |
| + |
|
| 极小值 |
|
∴当![]() 时,函数
时,函数![]() 取得最小值
取得最小值![]() ,∴
,∴![]() ,
,![]() ;
;
当![]() 时,函数
时,函数![]() 是增函数,在
是增函数,在![]() 没有最小值,当
没有最小值,当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 有最小值
有最小值![]() ,
,
∴![]() .
.
(2)![]() ,
,![]() ,设
,设![]() ,
,
∵![]() ,∴当
,∴当![]() 时
时![]() ,
,![]() 即
即![]() 单调递减,
单调递减,
当![]() 时
时![]() ,
,![]() 即
即![]() 单调递增,
单调递增,
由(1)得![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
![]() 时,
时,![]() ,
,![]() 单调递减,∴
单调递减,∴![]() 在
在![]() 有唯一极大值点
有唯一极大值点![]() ;
;
∵![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
∴在![]() 存在唯一实数
存在唯一实数![]() ,使得
,使得![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
∴函数![]() 在
在![]() 有唯一极小值点
有唯一极小值点![]() ;
;
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴存在自然数![]() ,使得函数
,使得函数![]() 的所有极值点之和
的所有极值点之和![]() .
.

【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 | 2017.8 | 2017.9 | 2017.10 | 2017.11 | 2017.12 | 2018.1 |
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市 场占有率y(%) | 11 | 13 | 16 | 15 | 20 | 21 |
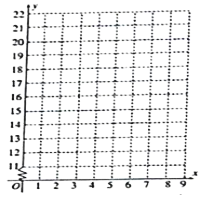
(1)请在给出的坐标纸中作出散点图;
(2)求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
参考公式:回归直线方程为![]() 其中:
其中: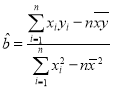 ,
,![]()
【题目】中国是世界互联网服务应用最好的国家,一部智能手机就可以跑遍国内所有地方,中国市场的移动支付普及率高得惊人.一家大型超市委托某高中数学兴趣小组调查该超市的顾客使用移动支付的情况,调查人员从年龄在![]() 内的顾客中,随机抽取了
内的顾客中,随机抽取了![]() 人,调查他们是否使用移动支付,结果如下表:
人,调查他们是否使用移动支付,结果如下表:
年龄 |
|
|
|
|
|
|
|
|
使用 |
|
|
|
|
|
|
|
|
不使用 |
|
|
|
|
|
|
|
|
(1)为更进一步推动移动支付,超市准备对使用移动支付的每位顾客赠送![]() 个环保购物袋,若某日该超市预计有
个环保购物袋,若某日该超市预计有![]() 人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关?
的把握认为使用移动支付与年龄有关?
年龄 | 年龄 | 小计 | |
使用移动支付 | |||
不使用移动支付 | |||
合计 |
附:下面的临界值表供参考:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
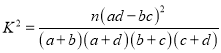 ,其中
,其中![]() .
.