��Ŀ����
����Ŀ������ʡ����������������֮����֮�ƣ����ʳ����з�������ĸ��ʺ�������ʢ�������㣬�ǻ������ں��е�����Ϊ![]() ���������ں��еĺ������ĵ�λ��Ϊ
���������ں��еĺ������ĵ�λ��Ϊ![]() �����о������������
����������������![]() ��
��![]() �����ȣ����ⶨ����������ĺ�����Ϊ200��λʱ��������Ϊ
�����ȣ����ⶨ����������ĺ�����Ϊ200��λʱ��������Ϊ![]() .
.
��1����![]() ����
����![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ
��2�����㻨���㾲ֹʱ�������ĵ�λ��.
��3�����ij������������������1![]() ����ô���ĺ������ĵ�λ����ԭ���Ķ��ٱ���
����ô���ĺ������ĵ�λ����ԭ���Ķ��ٱ���
���𰸡���1��![]() ����2��
����2��![]() ����3��4��
����3��4��
��������
��1������������ģ����ʽ����![]() ��������֪�������
��������֪�������![]() ���ã�
���ã�
��2����![]() ���
���![]() ��
��
��3����![]() ���
���![]() ��
��![]() �Ĺ�ϵ���ɣ�
�Ĺ�ϵ���ɣ�
��1���������������![]() ��
��![]() �����ȣ�����
�����ȣ�����![]()
����Ϊ��![]() ʱ��
ʱ��![]() ������
������![]() �����
�����![]()
����![]()
��2���������㾲ֹʱ��![]() ����
����![]() ���
���![]()
��3���軨���㿪ʼ���ٶȼ�Ϊ![]() �������ĵ�λ��Ϊ
�������ĵ�λ��Ϊ![]() ���������ٶȼ�Ϊ
���������ٶȼ�Ϊ![]() �������ٺ�ĺ����ĵ�λ��Ϊ
�������ٺ�ĺ����ĵ�λ��Ϊ![]()
��Ϊ![]()
����Ϊ![]() ��
��![]()
����![]() �����������ĵ�λ����ԭ����4��.
�����������ĵ�λ����ԭ����4��.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���������ij�豸��ʹ������x���꣩����֧����ά����y��Ԫ�����µ�ͳ�����ϣ�
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
��1������ɢ��ͼ���ж��Ƿ�������أ�
��2�����������أ������Իع鷽�̣�
��3������ʹ������Ϊ10��ʱ��ά�����Ƕ��٣�
��ע���ٲο���ʽ���ع鷽��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ ��
��
�ڲο����ݣ�![]()
����Ŀ��ij��˾Ϊ�˽���Ͷ������������Ӱ�죬�����ɵ�����Ͷ��4��Ԫ�����ã��������ص�����������Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�������ڹ�����Ա����ʧ��������ݶ�ʧ��������ȷ�������Ǵ�0��ʼ������.
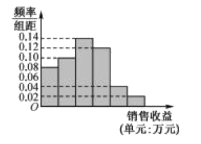
��1������Ƶ�ʷֲ�ֱ��ͼ����ͼ�и�С�����εĿ��ȣ�
��2���Թ��Ƹù�˾�����ɵ�����Ͷ��4��Ԫ������֮��Ӧ���������ƽ��ֵ���Ը���������е�ֵ���������ȡֵ����
��3���ù�˾�������Ƶ��о��������������һЩ���ݣ��������õ��±���
���Ͷ�� | 1 | 2 | 3 | 4 | 5 |
�������� | 2 | 3 | 3 | 7 |
�ɱ��е�������ʾ��![]() ��
��![]() ֮�������������ع�ϵ���뽫��2���Ľ������հ����������
֮�������������ع�ϵ���뽫��2���Ľ������հ����������![]() ����
����![]() �Ļع�ֱ�߷���.���ο���ʽ��
�Ļع�ֱ�߷���.���ο���ʽ��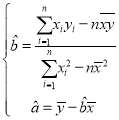 ��
��

