题目内容
已知函数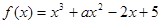
(1)若函数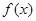 在
在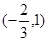 上单调递减,在
上单调递减,在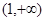 上单调递增,求实数
上单调递增,求实数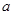 的值;
的值;
(2)是否存在实数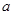 ,使得
,使得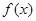 在
在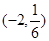 上单调递减,若存在,试求
上单调递减,若存在,试求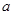 的取值范围;
的取值范围;
若不存在,请说明理由;
(3)若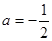 ,当
,当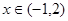 时不等式
时不等式 有解,求实数
有解,求实数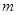 的取值范围.
的取值范围.
(1) ;(2)
;(2) ;(3)
;(3)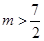 .
.
解析试题分析:
解题思路:(1)求导,利用条件可得出 ,解
,解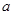 值;(2)求导,利用
值;(2)求导,利用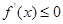 恒成立,得到
恒成立,得到 解得
解得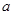 的范围;(3)当
的范围;(3)当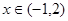 时不等式
时不等式 有解,即
有解,即 .
.
规律总结:若函数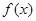 在某区间上单调递增,则
在某区间上单调递增,则 在该区间恒成立;“若函数
在该区间恒成立;“若函数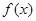 在某区间上单调递减,则
在某区间上单调递减,则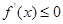 在该区间恒成立.
在该区间恒成立.
试题解析:(1) ,
,
∵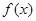 在
在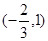 上单调递减,在
上单调递减,在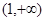 上单调递增,
上单调递增,
∴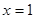 是方程
是方程 的根,解得
的根,解得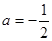
(2)由题意得: 上恒成立,
上恒成立,
∴
(3)当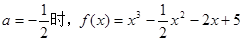 ,
,
由
列表: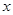
-1 (  )
)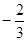
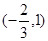
1 (1,2) 2 
+ 0 - 0 +  练习册系列答案
练习册系列答案
通城学典课时新体验系列答案
亮点给力提优课时作业本系列答案
神农牛皮卷期末考向标系列答案
金钥匙课课通系列答案
15天巧夺100分系列答案

课堂作业课时训练系列答案
名师点拨课时作业本系列答案
提优训练非常阶段123系列答案
高效课堂课时作业系列答案
相关题目
 ,2)时,(x-2)
,2)时,(x-2) >0.设a=f(1
>0.设a=f(1 ),
),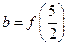 ,c=f(4),则a,b,c的大小为 .
,c=f(4),则a,b,c的大小为 .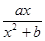 在x=1处取得极值2.
在x=1处取得极值2.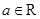 ,函数
,函数 (
( 为自然对数的底数).
为自然对数的底数).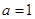 ,求函数
,求函数 的单调区间;
的单调区间; ,求
,求 .
. 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;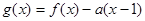 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中
上的最小值.(其中 为自然对数的底数)
为自然对数的底数)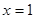 是函数
是函数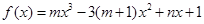 的一个极值点,其中
的一个极值点,其中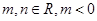 .
. 与
与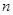 的关系式;
的关系式;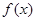 的单调区间;
的单调区间; 时,函数
时,函数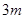 ,求
,求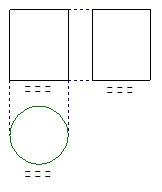
 (x)在(a,b)
(x)在(a,b) 
 象如图示,则函数f(x)在(a,b)内极小值点的个数为___________
象如图示,则函数f(x)在(a,b)内极小值点的个数为___________ 的导数为
的导数为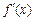 ,则
,则 = 。
= 。