题目内容
(本题满分14分)
某学校拟建一座长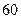 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?
某学校拟建一座长
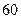 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 为何值时,所需总费用最少?
为何值时,所需总费用最少?每隔3米打建一个桩位时,所需总费用最小为1170万元.
由题意可知,需打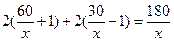 个桩位. …………3分
个桩位. …………3分
墙面所需费用为: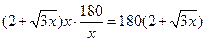 ,………………5分
,………………5分
∴所需总费用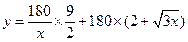
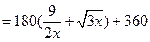 (
(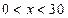 ) ………9分
) ………9分
令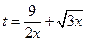 ,则
,则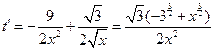 ,
,
当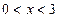 时,
时,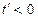 ;当
;当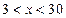 时,
时,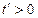 .∴当
.∴当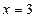 时,
时,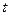 取极小值为
取极小值为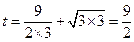 .
.
而在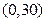 内极值点唯一,所以
内极值点唯一,所以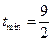 .∴当
.∴当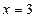 时,
时,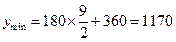 (万元),
(万元),
即每隔3米打建一个桩位时,所需总费用最小为1170万元. …………14分
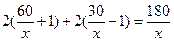 个桩位. …………3分
个桩位. …………3分墙面所需费用为:
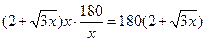 ,………………5分
,………………5分∴所需总费用
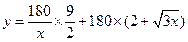
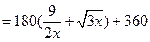 (
(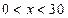 ) ………9分
) ………9分令
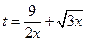 ,则
,则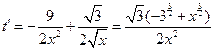 ,
,当
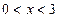 时,
时,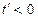 ;当
;当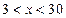 时,
时,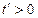 .∴当
.∴当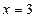 时,
时,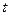 取极小值为
取极小值为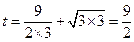 .
.而在
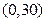 内极值点唯一,所以
内极值点唯一,所以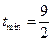 .∴当
.∴当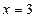 时,
时,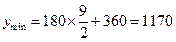 (万元),
(万元),即每隔3米打建一个桩位时,所需总费用最小为1170万元. …………14分

练习册系列答案
相关题目
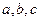
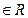 ,
,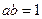 ,
,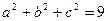 ,求
,求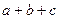 的最大值
的最大值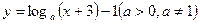 的图像恒过点A,若点A在直线
的图像恒过点A,若点A在直线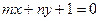 上,其中
上,其中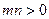 ,则
,则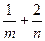 的最小值为 .
的最小值为 . ,
, 的最小值为
的最小值为 ,求
,求 的值
的值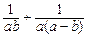 -10ac+25c2的最小值是 ( )
-10ac+25c2的最小值是 ( )
 对任意正实数
对任意正实数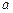 、
、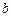 都成立,则
都成立,则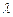 的最大值是( )
的最大值是( )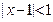 的解集是 .
的解集是 .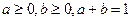 ,则
,则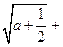
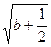 的范围是____________
的范围是____________