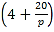题目内容
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:
满足:
①在区间![]() 上单调递减,②存在常数p,使其值域为
上单调递减,②存在常数p,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“逼进函数”.
的“逼进函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“逼进函数”;
的“逼进函数”;
(2)求证:函数![]() 不是函数
不是函数![]() ,的“逼进函数”
,的“逼进函数”
(3)若![]() 是函数
是函数![]() 的“逼进函数”,求a的值.
的“逼进函数”,求a的值.
【答案】(1)见解析; (2)见解析; (3)2.
【解析】
(1)由f(x)﹣g(x),化简整理,结合反比例函数的单调性和值域,即可判断;
(2)由指数函数和一次函数的单调性,可得满足①,说明不满足②,即可得证;
(3)由新定义,可得y=x![]() ax为[0,+∞)的减函数,求得导数,由不等式恒成立思想,可得a的范围;再由值域为(0,1],结合不等式恒成立思想可得a的范围,即可得到a的值.
ax为[0,+∞)的减函数,求得导数,由不等式恒成立思想,可得a的范围;再由值域为(0,1],结合不等式恒成立思想可得a的范围,即可得到a的值.
(1)![]()
![]() ,
,
可得![]() 在[0,+∞)递减,且
在[0,+∞)递减,且![]() ,
,
![]() ,可得存在
,可得存在![]() ,函数y的值域为
,函数y的值域为![]() ,
,
则函数![]() 是函数
是函数![]() ,
,![]() 的“逼进函数”;
的“逼进函数”;
(2)证明:![]() ,
,
由![]() ,
,![]() 在[0,+∞)递减,
在[0,+∞)递减,
则函数![]() 在[0,+∞)递减,
在[0,+∞)递减,
则函数![]() 在[0,+∞)的最大值为1;
在[0,+∞)的最大值为1;
由![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
则函数![]() 在[0,+∞)的值域为(-∞,1],
在[0,+∞)的值域为(-∞,1],
即有函数![]() 不是函数
不是函数![]() ,x∈[0,+∞)的“逼进函数”;
,x∈[0,+∞)的“逼进函数”;
(3)![]() 是函数
是函数![]() ,
,![]() 的“逼进函数”,
的“逼进函数”,
可得![]() 为[0,+∞)的减函数,
为[0,+∞)的减函数,
可得导数![]() 在[0,+∞)恒成立,
在[0,+∞)恒成立,
可得![]() ,
,
由x>0时,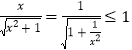 ,
,
则![]() ,即
,即![]() ;
;
又![]() 在[0,+∞)的值域为(0,1],
在[0,+∞)的值域为(0,1],
则![]() ,
,
x=0时,显然成立;
x>0时,![]() ,
,
可得![]() ,即
,即![]() .
.
则a=2.

 口算题天天练系列答案
口算题天天练系列答案【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源分时租赁汽车”.其中一款新能源分时租赁汽车,每次租车收费的标准由两部分组成:①根据行驶里程数按1元/公里计费;②行驶时间不超过![]() 分时,按
分时,按![]() 元/分计费;超过
元/分计费;超过![]() 分时,超出部分按
分时,超出部分按![]() 元/分计费.已知王先生家离上班地点
元/分计费.已知王先生家离上班地点![]() 公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间
公里,每天租用该款汽车上、下班各一次.由于堵车、红绿灯等因素,每次路上开车花费的时间 ![]() (分)是一个随机变量.现统计了
(分)是一个随机变量.现统计了![]() 次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
次路上开车花费时间,在各时间段内的频数分布情况如下表所示:
时间 |
|
|
|
|
频数 |
|
|
|
|
将各时间段发生的频率视为概率,每次路上开车花费的时间视为用车时间,范围为![]() 分.(1)写出王先生一次租车费用
分.(1)写出王先生一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分)的函数关系式;(2)若王先生一次开车时间不超过
(分)的函数关系式;(2)若王先生一次开车时间不超过![]() 分为“路段畅通”,设
分为“路段畅通”,设![]() 表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.
表示3次租用新能源分时租赁汽车中“路段畅通”的次数,求的分布列和期望.