题目内容
已知在平面直角坐标系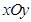 中,圆
中,圆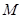 的方程为
的方程为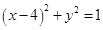 .以原点
.以原点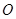 为极点,以
为极点,以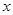 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线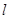 的极坐标方程为
的极坐标方程为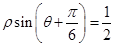 .
.
(1)求直线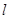 的直角坐标方程和圆
的直角坐标方程和圆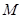 的参数方程;
的参数方程;
(2)求圆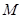 上的点到直线
上的点到直线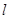 的距离的最小值.
的距离的最小值.
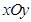 中,圆
中,圆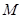 的方程为
的方程为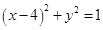 .以原点
.以原点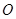 为极点,以
为极点,以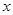 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线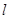 的极坐标方程为
的极坐标方程为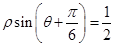 .
.(1)求直线
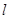 的直角坐标方程和圆
的直角坐标方程和圆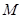 的参数方程;
的参数方程;(2)求圆
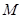 上的点到直线
上的点到直线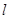 的距离的最小值.
的距离的最小值.(1)参考解析;(2)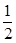
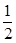
试题分析:(1)圆
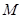 的方程为
的方程为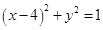 ,圆心为
,圆心为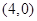 ,半径为1,根据直线的参数方程即可得到圆的参数方程.直线
,半径为1,根据直线的参数方程即可得到圆的参数方程.直线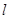 的极坐标方程为
的极坐标方程为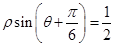 ,将三角函数展开,再根据极坐标与普通方程相互转化即可得结论.
,将三角函数展开,再根据极坐标与普通方程相互转化即可得结论.(2)圆
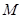 上的点到直线
上的点到直线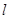 的距离的最小值,根据圆的参数参数方程,由点到直线的距离公式,再根据三角函数的性质得到的结论.
的距离的最小值,根据圆的参数参数方程,由点到直线的距离公式,再根据三角函数的性质得到的结论.(1)由
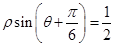 ,得
,得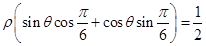 ,
,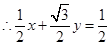 ,即
,即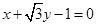 , 1分
, 1分设
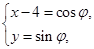
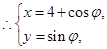 2分
2分所以直线
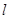 的直角坐标方程为
的直角坐标方程为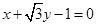 ;
;圆
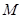 的参数方程
的参数方程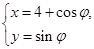
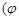 为参数
为参数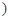 . 3分
. 3分(2)设
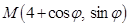 ,则点
,则点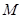 到直线
到直线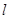 的距离为
的距离为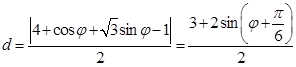 , 5分
, 5分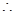 当
当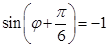 即
即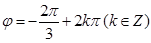 时,
时,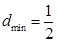 .
.圆
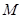 上的点到直线
上的点到直线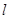 的距离的最小值为
的距离的最小值为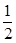 . 7分
. 7分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
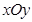 中,已知曲线
中,已知曲线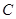 的参数方程是
的参数方程是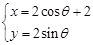 (
(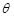 是参数),若以
是参数),若以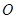 为极点,
为极点,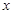 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线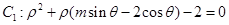 关于曲线
关于曲线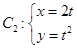 (
(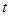 为参数)的准线对称,则
为参数)的准线对称,则  .
.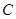 的参数方程为
的参数方程为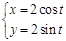 (
(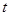 为参数),曲线
为参数),曲线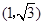 处的切线为
处的切线为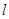 .以坐标原点为极点,
.以坐标原点为极点,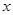 轴的正半轴为极轴建立极坐标系,求
轴的正半轴为极轴建立极坐标系,求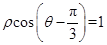 ,M,N分别为曲线C与x轴、y轴的交点.
,M,N分别为曲线C与x轴、y轴的交点.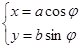 (a>b>0,
(a>b>0,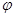 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M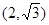 对应的参数
对应的参数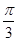 ,
,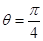 与曲线C2交于点D
与曲线C2交于点D
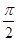 )是曲线C1上的两点,求
)是曲线C1上的两点,求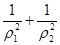 的值。
的值。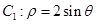 ,曲线
,曲线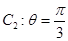 ,若曲线
,若曲线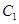 与
与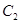 交于
交于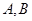 两点,则线段
两点,则线段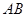 的长度为 .
的长度为 .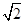 sin
sin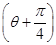 ,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为
,以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系,直线l的参数方程为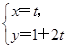 (t为参数),判断直线l和圆C的位置关系.
(t为参数),判断直线l和圆C的位置关系.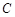 的极坐标方程为
的极坐标方程为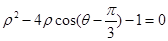 ,若以极点为原点,以极轴为
,若以极点为原点,以极轴为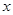 轴的正半轴建立相应的平面直角坐标系
轴的正半轴建立相应的平面直角坐标系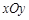 ,则在直角坐标系中,圆心
,则在直角坐标系中,圆心