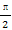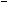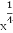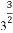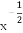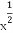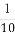题目内容
已知函数f(x)=a- 是偶函数,a为实常数.
是偶函数,a为实常数.
(1)求b的值.
(2)当a=1时,是否存在n>m>0,使得函数y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],若存在,求出m,n的值,否则,说明理由.
(1) b=0 (2) 不存在,理由见解析
【解析】(1)由已知,可得f(x)=a-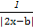 的定义域为D=(-∞,
的定义域为D=(-∞,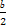 )∪(
)∪(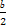 ,+∞).
,+∞).
又y=f(x)是偶函数,故定义域D关于原点对称.
于是,b=0(否则,当b≠0时,有-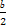 ∈D且
∈D且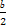
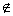 D,即D必不关于原点对称).
D,即D必不关于原点对称).
又对任意x∈D,有f(x)=f(-x),可得b=0
因此所求实数b=0.
(2)由(1),可知f(x)=a-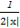 (D=(-∞,0)∪(0,+∞)).
(D=(-∞,0)∪(0,+∞)).
考察函数f(x)=a-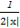 的图象,可知:f(x)在区间(0,+∞)上是增函数,
的图象,可知:f(x)在区间(0,+∞)上是增函数,
又n>m>0,
∴y=f(x)在区间[m,n]上是增函数.
因y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n].
∴有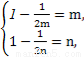
即方程1-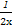 =x,也就是2x2-2x+1=0有两个不相等的正根.
=x,也就是2x2-2x+1=0有两个不相等的正根.
∵Δ=4-8<0,∴此方程无解.
故不存在正实数m,n满足题意.

练习册系列答案
相关题目