题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在定义域上是单调递增函数,求
在定义域上是单调递增函数,求![]() 的取值范围;
的取值范围;
(2)若![]() 恒成立,求
恒成立,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,利用导数研究函数的单调性,则![]() 在
在![]() 恒成立,可得
恒成立,可得![]() ,方法一:令
,方法一:令![]() 在
在![]() 恒成立,利用二次函数性质,即可求解参数范围;方法二:令
恒成立,利用二次函数性质,即可求解参数范围;方法二:令![]() 在
在![]() 恒成立,转化不等式
恒成立,转化不等式![]() ,利用基本不等式求解
,利用基本不等式求解![]() ,再根据恒成立思想,即可求解参数取值范围.
,再根据恒成立思想,即可求解参数取值范围.
(2)由题意,化简得![]() 在
在![]() 恒成立,令
恒成立,令![]() ,不难发现
,不难发现![]() ,即
,即![]() 在
在![]() 恒成立,根据极值点概念,判断
恒成立,根据极值点概念,判断![]() 是
是![]() 的极值,可求解参数值,检验成立.
的极值,可求解参数值,检验成立.
(1)函数![]() 在定义域上是单调递增函数,可知导函数
在定义域上是单调递增函数,可知导函数![]() 在
在![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,
恒成立,
可得![]()
方法一:令![]() 在
在![]() 恒成立,
恒成立,
①当对称轴![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]() ,即
,即![]() 恒成立;
恒成立;
②当对称轴![]() ,结合二次函数的性质要使在
,结合二次函数的性质要使在![]() 恒成立,
恒成立,![]() ,
,
即![]() ,解得
,解得![]()
综上可得![]() 的取值范围是
的取值范围是![]() ;
;
方法二:令![]() 在
在![]() 恒成立,
恒成立,
可得![]()
即![]() 在
在![]() 恒成立,
恒成立,
![]()
![]() ,
,
![]() ,
,
即![]() ,
,
故![]() 的取值范围是
的取值范围是![]() ;
;
(2)由题意![]() 恒成立,
恒成立,
即![]() 在
在![]() 恒成立,
恒成立,
令![]() ,
,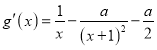
不难发现![]() ,即
,即![]()
那么![]() 时,
时,![]() 取得最大值,也是极大值,
取得最大值,也是极大值,
可知![]() 是导函数的一个解.
是导函数的一个解.
即![]() ,
,
解得![]()
经检验,当![]() 时,
时,![]() 在
在![]() 递增,在
递增,在![]() 递减,从而
递减,从而![]() 成立,符合题意,
成立,符合题意,
故得![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布表,其中![]() .(计算结果保留两位小数)
.(计算结果保留两位小数)
分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频率 | 0.08 |
| 0.35 | 0.27 |
|
(1)试估计被调查的员工的满意程度的中位数;
(2)若把每组的组中值作为该组的满意程度,试估计被调查的员工的满意程度的平均数.