题目内容
【题目】设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形: 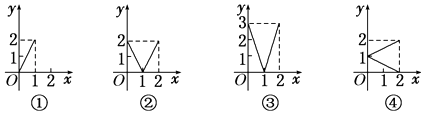
其中,能表示从集合M到集合N的函数关系的个数是( )
A.0
B.1
C.2
D.3
【答案】B
【解析】解:①中,因为在集合M中当1<x≤2时,在N中无元素与之对应,所以①不是;
②中,对于集合M中的任意一个数x,在N中都有唯一的数与之对应,所以②是;
③中,x=2对应元素y=3N,所以③不是;
④中,当x=1时,在N中有两个元素与之对应,所以④不是.因此只有②满足题意.
故选B.
【考点精析】本题主要考查了函数的概念及其构成要素的相关知识点,需要掌握函数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数才能正确解答此题.

练习册系列答案
相关题目
【题目】国家为了鼓励节约用水,实行阶梯用水收费制度,价格参照表如表:
用水量(吨) | 单价(元/吨) | 注 |
0~20(含) | 2.5 | |
20~35(含) | 3 | 超过20吨不超过35吨的部分按3元/吨收费 |
35以上 | 4 | 超过35吨的部分按4元/吨收费 |
(1)若小明家10月份用水量为30吨,则应缴多少水费?
(2)若小明家10月份缴水费99元,则小明家10月份用水多少吨?
(3)写出水费y与用水量x之间的函数关系式,并画出函数的图象.