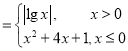题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线
的直线与抛物线![]() 相切,设第一象限的切点为
相切,设第一象限的切点为![]() .
.
(Ⅰ)证明:点![]() 在
在![]() 轴上的射影为焦点
轴上的射影为焦点![]() ;
;
(Ⅱ)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于两点
相交于两点![]() ,圆
,圆![]() 是以线段
是以线段![]() 为直径的圆且过点
为直径的圆且过点![]() ,求直线
,求直线![]() 与圆
与圆![]() 的方程.
的方程.
【答案】(I)详见解析;(II)详见解析.
【解析】
(Ⅰ)设过点![]() 的直线方程为
的直线方程为![]() ,与抛物线方程联立消元后得到二次方程,根据判别式为零得到
,与抛物线方程联立消元后得到二次方程,根据判别式为零得到![]() ,当
,当![]() 时可求得点
时可求得点![]() 坐标为
坐标为![]() ,而焦点为
,而焦点为![]() ,故结论成立.(Ⅱ)设直线
,故结论成立.(Ⅱ)设直线![]() 的方程为
的方程为![]() ,与抛物线方程联立消元后得到二次方程.由圆
,与抛物线方程联立消元后得到二次方程.由圆![]() 是以线段
是以线段![]() 为直径的圆且过点
为直径的圆且过点![]() 可得
可得![]() ,然后结合根与系数的关系求出
,然后结合根与系数的关系求出![]() 或
或![]() ,进而可得所求方程.
,进而可得所求方程.
(Ⅰ)由题意知可设过点![]() 的直线方程为
的直线方程为![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() ,
,
又因为直线与抛物线相切,
所以![]() ,解得
,解得![]() .
.
当![]() 时,直线方程为
时,直线方程为![]() ,可得点
,可得点![]() 坐标为
坐标为![]() ,
,
又因为焦点![]() ,
,
所以点![]() 在
在![]() 轴上的射影为焦点
轴上的射影为焦点![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由![]() ,
,
其中![]() 恒成立.
恒成立.
设![]() ,
,![]() ,
,
则![]() ,
,
所以![]() ,
,![]() .
.
由于圆![]() 是以线段
是以线段![]() 为直径的圆过点
为直径的圆过点![]() ,则
,则![]() ,
,
所以![]()
所以![]() ,
,
解得![]() 或
或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
【题目】某校2019届高三年级参加市高考模拟考试的学生有1000人,随机抽取了一个容量为200的学生总成绩(满分750分)的样本,各分数段人数如表所示:
分数段 |
|
|
|
|
|
人数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)若本次模拟考试一本的预测分数线为550分,试估计该校的一本上线人数.