题目内容
4.解不等式$\frac{\sqrt{{x}^{2}+1}+{2}^{x}}{\sqrt{{x}^{2}+1}+{2}^{x+1}}$+$\frac{\sqrt{{x}^{2}+2}+{3}^{2x}}{\sqrt{{x}^{2}+2}+{3}^{2x+1}}$+$\frac{\sqrt{{x}^{2}+3}+{6}^{3x}}{\sqrt{{x}^{2}+3}+{6}^{3x+1}}$>1.分析 根据不等式若a,b,m∈R+,且a<b,则不等式$\frac{a+m}{b+m}$>$\frac{a}{b}$的结论,进行求解即可.
解答 解:已知若a,b,m∈R+,且a<b,
则不等式$\frac{a+m}{b+m}$>$\frac{a}{b}$,
则$\frac{\sqrt{{x}^{2}+1}+{2}^{x}}{\sqrt{{x}^{2}+1}+{2}^{x+1}}$>$\frac{{2}^{x}}{{2}^{x+1}}$=$\frac{1}{2}$,
$\frac{\sqrt{{x}^{2}+2}+{3}^{2x}}{\sqrt{{x}^{2}+2}+{3}^{2x+1}}$>$\frac{{3}^{2x}}{{3}^{2x+1}}$=$\frac{1}{3}$,
$\frac{\sqrt{{x}^{2}+3}+{6}^{3x}}{\sqrt{{x}^{2}+3}+{6}^{3x+1}}$>$\frac{{6}^{3x}}{{6}^{3x+1}}$=$\frac{1}{6}$,
则$\frac{\sqrt{{x}^{2}+1}+{2}^{x}}{\sqrt{{x}^{2}+1}+{2}^{x+1}}$+$\frac{\sqrt{{x}^{2}+2}+{3}^{2x}}{\sqrt{{x}^{2}+2}+{3}^{2x+1}}$+$\frac{\sqrt{{x}^{2}+3}+{6}^{3x}}{\sqrt{{x}^{2}+3}+{6}^{3x+1}}$>$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$=1,
即$\frac{\sqrt{{x}^{2}+1}+{2}^{x}}{\sqrt{{x}^{2}+1}+{2}^{x+1}}$+$\frac{\sqrt{{x}^{2}+2}+{3}^{2x}}{\sqrt{{x}^{2}+2}+{3}^{2x+1}}$+$\frac{\sqrt{{x}^{2}+3}+{6}^{3x}}{\sqrt{{x}^{2}+3}+{6}^{3x+1}}$>1恒成立,
即原不等式的解集为R.
点评 本题主要考查不等式的求解,根据不等式若a,b,m∈R+,且a<b,则不等式$\frac{a+m}{b+m}$>$\frac{a}{b}$的结论是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 13 | B. | 53 | C. | 81 | D. | 161 |
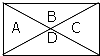 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |
| A. | f(x)=x3 | B. | f(x)=-|x+1| | C. | f(x)=ln$\frac{2-x}{2+x}$ | D. | f(x)=$\frac{{a}^{x}+{a}^{-x}}{2}$ |