题目内容
【题目】已知数列{an}与{bn}满足an+1﹣an=2(bn+1﹣bn),n∈N+ , bn=2n﹣1,且a1=2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,Tn为数列{cn}的前n项和,求Tn .
,Tn为数列{cn}的前n项和,求Tn .
【答案】解:(Ⅰ)∵bn=2n﹣1,∴bn+1﹣bn=2n+1﹣2n+1=2,
∴an+1﹣an=2(bn+1﹣bn)=4,
∴{an}是以a1=2为首项,以4为公差的等差数列,
∴an=2+4(n﹣1)=4n﹣2.
(Ⅱ) ![]() .
.
∴Tn=c1+c2+c3+…+cn=12+322+523+…+(2n﹣1)2n,①
∴ ![]() ,②
,②
①﹣②得: ![]() =
= ![]() =﹣6﹣(2n﹣3)2n+1,
=﹣6﹣(2n﹣3)2n+1,
∴ ![]() .
.
【解析】(Ⅰ)由题意利用递推公式可得出{an}是以a1=2为首项,以4为公差的等差数列进而可求出通项公式。(Ⅱ)整理已知的代数式根据题意求出{cn}的前n项和Tn,利用等式两边同时乘以公比两式相减即可得出{cn}的前n项和Tn。
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系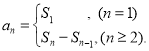 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

练习册系列答案
相关题目