题目内容
【题目】已知数列{an}满足a2=1,|an+1﹣an|= ![]() ,若a2n+1>a2n﹣1 , a2n+2<a2n(n∈N+)则数列{(﹣1)nan}的前40项的和为( )
,若a2n+1>a2n﹣1 , a2n+2<a2n(n∈N+)则数列{(﹣1)nan}的前40项的和为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵数列{an}满足a2=1,|an+1﹣an|= ![]() ,则an+1﹣an=±
,则an+1﹣an=± ![]() ,
,
an+2﹣an+1= ![]() .∴an+2﹣an=±
.∴an+2﹣an=± ![]() ±
± ![]() ,∵
,∵ ![]() >
> ![]() ,
,
n为偶数时,a2n+2<a2n(n∈N+),∴a2n+2﹣a2n=﹣ ![]() ±
± ![]() ,
,
n为奇数时,a2n+1>a2n﹣1,∴a2n+1﹣a2n﹣1= ![]() ±
± ![]() ,
,
综上可得:n为偶数时,an+1﹣an=﹣ ![]() ,
,
n为奇数时,an+1﹣an= ![]() .
.
∴数列{(﹣1)nan}的前40项=(a2﹣a1)+(a4﹣a3)+…+(a40﹣a39)
= ![]() +…+
+…+ ![]()
= ![]() +…+
+…+ ![]()
= ![]()
= ![]() .
.
所以答案是:D.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系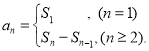 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目