Question

【题目】已知中心在坐标原点的椭圆 的长轴的一个端点是抛物线 的焦点，且椭圆 的离心率是 .
（1）求椭圆 的方程；
（2）过点 的动直线与椭圆 相交于 两点.若线段 的中点的横坐标是 ，求直线 的方程.

Answer 1

【答案】
（1）解：由题知椭圆 的焦点在 轴上，且 ，

又 ，故 ，

故椭圆 的方程为 ，即 .

（2）解：依题意，直线 的斜率存在，设直线 的方程为 ，将其代入 ，

消去 ，整理得 .

设 两点坐标分别为 ， .

则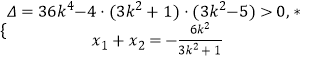

由线段 中点的横坐标是 ，得 ，

解得 ，符合（*）式.

所以直线 的方程为 或 .

【解析】（1）由已知条件得到关于a,b,c的方程组求a,b,c得到椭圆方程。
（2）将直线方程代入到椭圆方程中，消去y得关于x的一元二次方程，由韦达定理得到两根之和就是弦中点的横坐标，从而 求出直线的斜率得到方程。