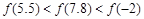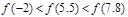题目内容
已知函数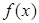 是定义在
是定义在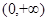 上的单调函数,且对任意的正数
上的单调函数,且对任意的正数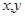 都有
都有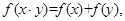 若数列
若数列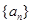 的前
的前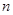 项和为
项和为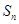 ,且满足
,且满足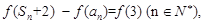 则
则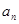 为( )
为( )
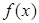 是定义在
是定义在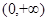 上的单调函数,且对任意的正数
上的单调函数,且对任意的正数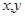 都有
都有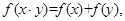 若数列
若数列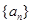 的前
的前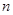 项和为
项和为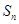 ,且满足
,且满足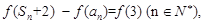 则
则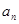 为( )
为( )A. | B. | C. | D. |
D
试题分析:因为对任意的正数x,y都有
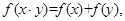
又
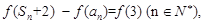 ,所以f(sn+2)=f(3)+f(an)=f(3•an),
,所以f(sn+2)=f(3)+f(an)=f(3•an),因为函数f(x)是定义在(0,+∞)上的单调函数,
所以sn+2=3an………………………………①
当n=1时,s1+2=a1+2=3a1,解得an=1;
当n≥2时,sn-1+2=3an-1………………②
①-②得:an=3an-3an-1
即
 ,所以数列{an}是一个以1为首项,以
,所以数列{an}是一个以1为首项,以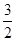 为公比的等比数列,所以
为公比的等比数列,所以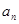 =
= 。
。点评:本题以抽象函数为载体考查了等比数列通项公式的求法,其中根据已知得到f(sn+2)=f(3)+f(an)=f(3•an)是解答的关键。

练习册系列答案
相关题目
 ,
, 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为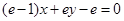 ,
,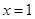 既是函数
既是函数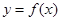 的零点,又是它的极值点.
的零点,又是它的极值点.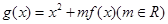 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围; 的单调递减区间,并证明:
的单调递减区间,并证明: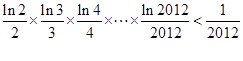
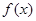 ,在使
,在使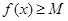 成立的所有常数M中,我们把M的最大值称为函数
成立的所有常数M中,我们把M的最大值称为函数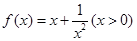 上的“下确界”为 .
上的“下确界”为 .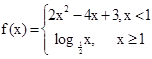 ,若
,若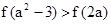 成立,则
成立,则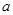 的取值范围是
的取值范围是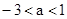
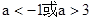

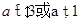
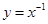 ,
,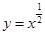 ,
,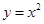 ,
,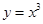 ,,
,,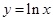 ,
,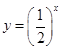 中,在区间
中,在区间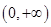 上为减函数的是_________.
上为减函数的是_________.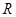 上的函数
上的函数 ,如果存在函数
,如果存在函数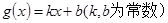 ,使得
,使得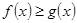 对一切实数
对一切实数 都成立,则称
都成立,则称 是函数
是函数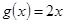 是
是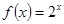 的一个“亲密函数”;
的一个“亲密函数”;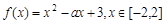 。
。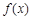 在
在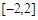 上的最小值是
上的最小值是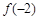 ,试解不等式
,试解不等式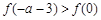 ;
;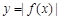 在
在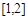 上单调递增,试求实数
上单调递增,试求实数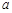 的取值范围。
的取值范围。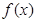 在区间[2,6]上是增函数,且最小值为4,则
在区间[2,6]上是增函数,且最小值为4,则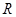 上的函数
上的函数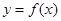 满足下列条件:①对任意的
满足下列条件:①对任意的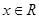 都有
都有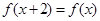 ;②若
;②若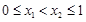 ,都有
,都有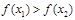 ;③
;③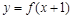 是偶函数,则下列不等式中正确的是()
是偶函数,则下列不等式中正确的是()