题目内容
【题目】已知p:x∈R,cos2x﹣sinx+2≤m;q:函数 ![]() 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
(I)若p∧q为真命题,求m的取值范围;
(II)若p∨q为真命题,p∧q为假命题,求m的取值范围.
【答案】解:若p为真,
令f(x)=cos2x﹣sinx+2,则m≥f(x)min ,
又f(x)=cos2x﹣sinx+2=cos2x﹣sinx+2=﹣2sin2x﹣sinx+3
又﹣1≤sinx≤1,
所以sinx=1时,
f(x)min=0,
所以m≥0
若q为真:
函数 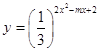 在[1,+∞)上单调递减,
在[1,+∞)上单调递减,
则 ![]() ,
,
所以m≤4
①若p∧q为真,则p,q均为真,所以m∈[0,4];②若p∨q为真,p∧q为假,则p,q一真一假,即 ![]() 即m>4
即m>4
或 ![]() 即m<0
即m<0
所以m的取值范围为(﹣∞,0)∪(4,+∞)
【解析】先求出命题p,q为真时,m的取值范围,( I)若p∧q为真命题,求两个范围的交集即可得到m的取值范围;( II)若p∨q为真命题,p∧q为假命题,则p,q一真一假,进而可得m的取值范围.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】为了检测某种产品的质量(单位:千克),抽取了一个容量为N的样本,整理得到的数据作出了频率分布表和频率分布直方图如图:
分组 | 频数 | 频率 |
[17.5,20) | 10 | 0.05 |
[20,225) | 50 | 0.25 |
[22.5,25) | a | b |
[25,27.5) | 40 | c |
[27.5,30] | 20 | 0.10 |
合计 | N | 1 |
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求频率分布直方图中d的值;
(Ⅲ)从该产品中随机抽取一件,试估计这件产品的质量少于25千克的概率.