题目内容
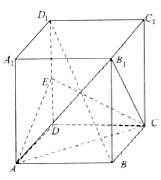
【题目】如图,已知长方形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)求证: ![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在何位置时,二面角
在何位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.
【答案】(1)(见解析2)见解析
【解析】试题分析:(1)先利用平面几何知识得到线线垂直,再利用面面垂直的性质得到线面垂直,进而得到线线垂直;(2)建立空间直角坐标系,利用向量共线得到有关点的坐标,再利用空间向量进行求解.
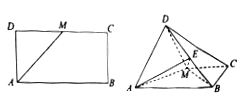
试题解析:(1)证明: ![]() 长方形
长方形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点,
![]() ,
, ![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 平面ADM
平面ADM
![]() .
.
(2)建立如图所示的直角坐标系
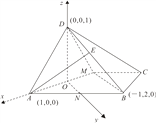
设![]() ,则平面
,则平面![]() 的一个法向量
的一个法向量![]() ,
,
![]()
![]() ,
,![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,则
,则
![]()
取![]() ,得
,得![]() ,
, ![]() ,
, ![]() 所以
所以![]() ,
,
因为, ![]()
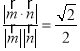 .得
.得![]() 或
或![]()
经检验得![]() 满足题意,所以
满足题意,所以![]() 为
为![]() 的三等分点.
的三等分点.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响