题目内容
在平面直角坐标系xOy中,点P到两点 ,
,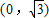 的距离之和等于4,设点P的轨迹为C.
的距离之和等于4,设点P的轨迹为C.(Ⅰ)写出C的方程;
(Ⅱ)设直线y=kx+1与C交于A,B两点.k为何值时
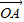 ⊥
⊥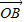 ?此时
?此时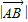 的值是多少?.
的值是多少?.
【答案】分析:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是椭圆.从而写出其方程即可;
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足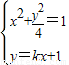 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时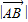 的值,从而解决问题.
的值,从而解决问题.
解答:解:
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以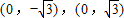 为焦点,
为焦点,
长半轴为2的椭圆.它的短半轴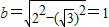 ,
,
故曲线C的方程为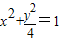 .(4分)
.(4分)
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足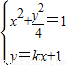
消去y并整理得(k2+4)x2+2kx-3=0,
故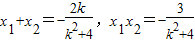 .(6分)
.(6分)
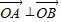 ,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
于是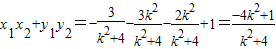 .
.
所以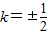 时,x1x2+y1y2=0,故
时,x1x2+y1y2=0,故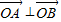 .(8分)
.(8分)
当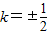 时,
时,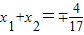 ,
,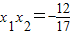 .
.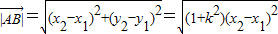 ,
,
而(x2-x1)2=(x2+x1)2-4x1x2=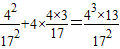 ,
,
所以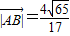 .(12分)
.(12分)
点评:本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.
(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足
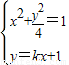 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系及向量垂直的条件,求出k值即可,最后通牒利用弦长公式即可求得此时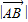 的值,从而解决问题.
的值,从而解决问题.解答:解:
(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以
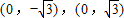 为焦点,
为焦点,长半轴为2的椭圆.它的短半轴
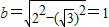 ,
,故曲线C的方程为
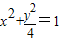 .(4分)
.(4分)(Ⅱ)设A(x1,y1),B(x2,y2),其坐标满足
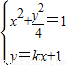
消去y并整理得(k2+4)x2+2kx-3=0,
故
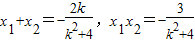 .(6分)
.(6分)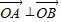 ,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,
,即x1x2+y1y2=0.而y1y2=k2x1x2+k(x1+x2)+1,于是
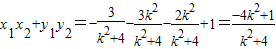 .
.所以
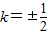 时,x1x2+y1y2=0,故
时,x1x2+y1y2=0,故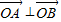 .(8分)
.(8分)当
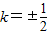 时,
时,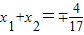 ,
,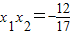 .
.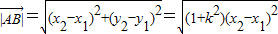 ,
,而(x2-x1)2=(x2+x1)2-4x1x2=
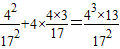 ,
,所以
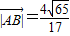 .(12分)
.(12分)点评:本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是