题目内容
【题目】已知![]() ,
, ![]() 。
。
(1)写出![]() 的解析式与定义域;
的解析式与定义域;
(2)画出函数![]() 的图像;
的图像;
(3)试讨论方程![]() 的根的个数。
的根的个数。
【答案】(1)定义域![]()
 (2)见解析(3)
(2)见解析(3)![]() 时,方程有一解;
时,方程有一解; ![]() 时,方程有两解;
时,方程有两解; ![]() 时,方程无解。
时,方程无解。
【解析】试题分析:(1)根据表达式,得出函数f(x)的定义域是(﹣2,+∞),将H(x)化成分段函数的形式.
(2)得到函数y=H(x﹣1)+2的分段表达式,进而可以作出它的图象;
(3)根据图象可以得到,当m=2或m≥10时,直线y=m与函数y=H(x﹣1)+2图象有且仅有一个公共点;当2<m<10时,直线y=m与函数y=H(x﹣1)+2图象有两个公共点;当m<2时,直线y=m与函数y=H(x﹣1)+2图象没有公共点.由此则不难得出方程根的个数了.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, 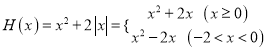
(2)![]() =
= ,
,
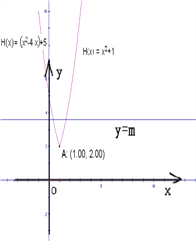
(3)在同一坐标系里作出直线y=m,观察它与函数y=H(x)图象的交点的个数,可得
①当m=2或m≥10时,直线y=m与函数y=H(x﹣1)+2图象有且仅有一个公共点;②当2<m<10时,直线y=m与函数y=H(x﹣1)+2图象有两个公共点;③当m<2时,直线y=m与函数y=H(x﹣1)+2图象没有一个公共点
由此可得:当m∈{2}∪[10,+∞)时,方程H(x﹣1)+2=m有且仅有一个实数根;
![]() 时,方程有一解;
时,方程有一解;
![]() 时,方程有两解;
时,方程有两解; ![]() 时,方程无解。
时,方程无解。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目