题目内容
.由a,b,c,d,e这5个字母排成一排,a,b都不与c相邻的排法个数为 ( )
| A.36 | B.32 | C.28 | D.24 |
A
专题:计算题;分类讨论.
分析:a,b都不与c可以分成两种情况,一是三个都不相邻,二是a,b相邻,但是不和c相邻,当三个都不相邻时,先排列d,e,再把三个元素插空,当a,b相邻,但是不和c相邻时,把a,b看成一个元素,插空排列,注意本身还有一个排列.
解答:解:a,b都不与c可以分成两种情况,
一是三个都不相邻,二是a,b相邻,但是不和c相邻,
当三个都不相邻时,先排列d,e,再把三个元素插空,有A22A33=12
当a,b相邻,但是不和c相邻时,有A22A32A22=24,
根据分类计数原理知,共有12+24=36种结果,
故选A
点评:本题考查排列组合的实际应用,考查带有限制条件的元素的排列问题,本题是一个易错题,易错点在a,b都不和c相邻,但是这两个元素可以相邻,容易漏掉这种情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
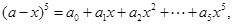 若
若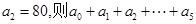 =
= 放入一个小球,则
放入一个小球,则 恰好有5个小球的标号与其所在的盒子的标号一致的方法总数为
恰好有5个小球的标号与其所在的盒子的标号一致的方法总数为
