题目内容
.数列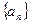 的各项均为正数,
的各项均为正数,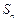 为其前
为其前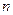 项和,对于任意
项和,对于任意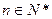 ,总有
,总有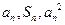 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列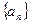 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列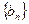 的前
的前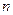 项和为
项和为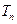 ,且
,且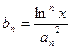 ,求证:对任意实数
,求证:对任意实数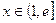 (
(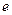 是常数,
是常数,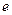 =2.71828
=2.71828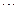 )和任意正整数
)和任意正整数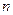 ,总有
,总有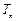
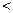 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列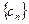 中,
中,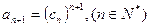 .求数列
.求数列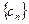 中的最大项.
中的最大项.
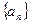 的各项均为正数,
的各项均为正数,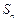 为其前
为其前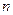 项和,对于任意
项和,对于任意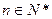 ,总有
,总有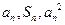 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列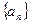 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列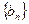 的前
的前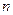 项和为
项和为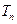 ,且
,且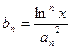 ,求证:对任意实数
,求证:对任意实数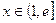 (
(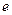 是常数,
是常数,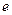 =2.71828
=2.71828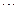 )和任意正整数
)和任意正整数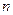 ,总有
,总有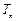
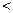 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列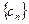 中,
中,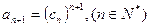 .求数列
.求数列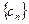 中的最大项.
中的最大项.(Ⅰ) 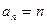 (Ⅱ) 略 (Ⅲ)
(Ⅱ) 略 (Ⅲ)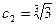
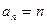 (Ⅱ) 略 (Ⅲ)
(Ⅱ) 略 (Ⅲ)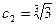
(Ⅰ)解:由已知:对于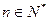 ,总有
,总有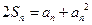 ①成立∴
①成立∴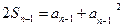
(n ≥ 2)② …1分
①--②得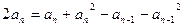 ∴
∴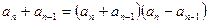
∵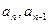 均为正数,∴
均为正数,∴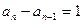 (n ≥ 2) ∴数列
(n ≥ 2) ∴数列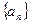 是公差为1的等差数列…3分又n=1时,
是公差为1的等差数列…3分又n=1时,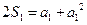 , 解得
, 解得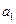 =1∴
=1∴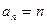 .(
.(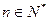 ) …5分
) …5分
(Ⅱ)证明:∵对任意实数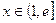 和任意正整数n,总有
和任意正整数n,总有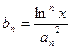 ≤
≤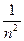 .……6分
.……6分
∴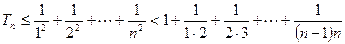
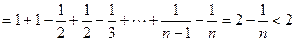 …9分
…9分
(Ⅲ)解:由已知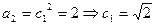 ,
,

易得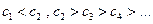 猜想 n≥2 时,
猜想 n≥2 时,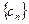 是递减数列. …11分
是递减数列. …11分
令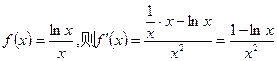
∵当
∴在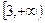 内
内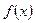 为单调递减函数.
为单调递减函数.
由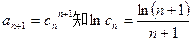 .
.
∴n≥2 时,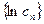 是递减数列.即
是递减数列.即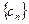 是递减数列.
是递减数列.
又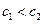 , ∴数列
, ∴数列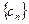 中的最大项为
中的最大项为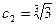 .…13分
.…13分
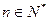 ,总有
,总有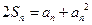 ①成立∴
①成立∴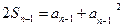
(n ≥ 2)② …1分
①--②得
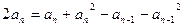 ∴
∴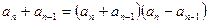
∵
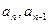 均为正数,∴
均为正数,∴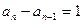 (n ≥ 2) ∴数列
(n ≥ 2) ∴数列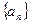 是公差为1的等差数列…3分又n=1时,
是公差为1的等差数列…3分又n=1时,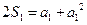 , 解得
, 解得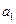 =1∴
=1∴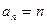 .(
.(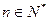 ) …5分
) …5分(Ⅱ)证明:∵对任意实数
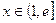 和任意正整数n,总有
和任意正整数n,总有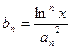 ≤
≤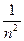 .……6分
.……6分∴
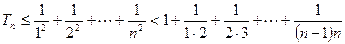
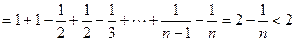 …9分
…9分(Ⅲ)解:由已知
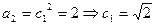 ,
,
易得
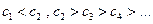 猜想 n≥2 时,
猜想 n≥2 时,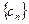 是递减数列. …11分
是递减数列. …11分令
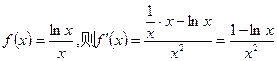
∵当

∴在
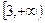 内
内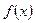 为单调递减函数.
为单调递减函数.由
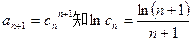 .
.∴n≥2 时,
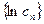 是递减数列.即
是递减数列.即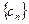 是递减数列.
是递减数列.又
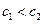 , ∴数列
, ∴数列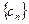 中的最大项为
中的最大项为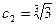 .…13分
.…13分
练习册系列答案
相关题目
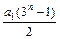 (对于所有n≥1),且a4=54,则a1的数值是_____.
(对于所有n≥1),且a4=54,则a1的数值是_____.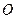 为
为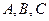 三点所在直线外一点,且
三点所在直线外一点,且 .数列
.数列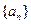 ,
,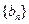 满足
满足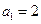 ,
,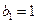 ,且
,且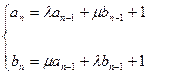 (
(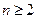 ).(Ⅰ) 求
).(Ⅰ) 求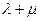 ;(Ⅱ) 令
;(Ⅱ) 令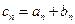 ,求数列
,求数列 的通项公式;(III) 当
的通项公式;(III) 当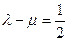 时,求数列
时,求数列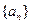 的前
的前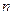 项和为
项和为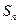 ,且对任意正整数
,且对任意正整数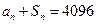 ,
,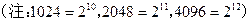 。(1)求数列
。(1)求数列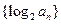 的前
的前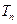 ,对数列
,对数列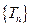 ,从第几项起
,从第几项起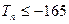 ?
?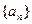 满足
满足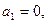
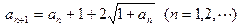 ,则
,则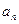 =___ .
=___ .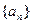 的前n项和为Sn,点
的前n项和为Sn,点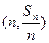 的直线
的直线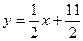 上,数列
上,数列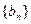 满足
满足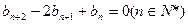 ,
,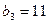 ,且
,且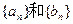 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设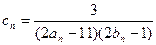 ,记数列
,记数列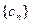 的前n项和为Tn,求使不等式
的前n项和为Tn,求使不等式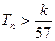 对一切
对一切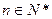 都成立的最大正整数k的值.
都成立的最大正整数k的值.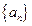 中,
中,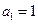 ,
,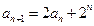 ;
;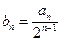 .证明:数列
.证明:数列 是等差数列;(2)求数列
是等差数列;(2)求数列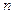 项和
项和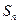 。
。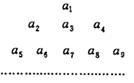
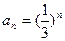 ,把数列{an}的各项排成如右图所示三角形形状,记
,把数列{an}的各项排成如右图所示三角形形状,记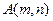 表示第m行、第n列的项,则
表示第m行、第n列的项,则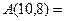 ,
,