题目内容
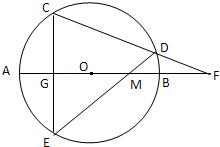 如图,已知AB是⊙O的直径,过OA的中点G作弦CE⊥AB于G,点D为优弧CBE上(除点B外)一动点,过D分别作直线CD,ED交直线AB于点F,M.
如图,已知AB是⊙O的直径,过OA的中点G作弦CE⊥AB于G,点D为优弧CBE上(除点B外)一动点,过D分别作直线CD,ED交直线AB于点F,M.(I)求∠FDM的值.
(II)若⊙O的直径长为4,M为OB的中点,求△CED的面积.
分析:(I)欲求∠FDM的值,由于此角不在圆内且与题设中条件联系不密切,故可将求此角的大小问题转化为求其补角角CDE的大小,由题设条件知G是半径的中点,由可在三角形COE中求出角EOC的大小,再由圆周角与圆心角的关系可以求得角CDE的大小,故可求得∠FDM的值.
(II)在三角形CDE中,角CDE已知,CE长度已知,在直角三角形EGM中可以求得角E的正弦,由此由正弦定理可以求出CD的长,再由正弦的和角公式求出角C的正弦,利用S=
×CE×CD×sinC,求其面积即可.
(II)在三角形CDE中,角CDE已知,CE长度已知,在直角三角形EGM中可以求得角E的正弦,由此由正弦定理可以求出CD的长,再由正弦的和角公式求出角C的正弦,利用S=
| 1 |
| 2 |
解答:解:(I)由题设条件过OA的中点G作弦CE⊥AB于G,连接OC,OE,
知OG=
OE=
OC,故可得∠OCG=∠OEG=30°,所以∠COE=120°,
∠CDM=60°,由图知∠FDM=120°,
(II)由题设⊙O的直径长为4,M为OB的中点
故GM=2,OG=1,
在直角三角形OGE中,由勾股定理可以求得GE=
,故EC=2
故可在直角三角形MGE中求得EM=
由此得sinE=
,cosE=
又∠CDE=60°
故sinC=sin(E+600)=
×
+
×
=
由正弦定理得CD=
×
=
DE=
×
=
故△CED的面积为
×
×
×
=
知OG=
| 1 |
| 2 |
| 1 |
| 2 |
∠CDM=60°,由图知∠FDM=120°,

(II)由题设⊙O的直径长为4,M为OB的中点
故GM=2,OG=1,
在直角三角形OGE中,由勾股定理可以求得GE=
| 3 |
| 3 |
故可在直角三角形MGE中求得EM=
| 7 |
由此得sinE=
2
| ||
| 7 |
| ||
| 7 |
又∠CDE=60°
故sinC=sin(E+600)=
2
| ||
| 7 |
| 1 |
| 2 |
| ||
| 7 |
| ||
| 2 |
5
| ||
| 14 |
由正弦定理得CD=
2
| ||||
|
2
| ||
| 7 |
8
| ||
| 7 |
DE=
2
| ||||
|
5
| ||
| 14 |
10
| ||
| 7 |
故△CED的面积为
| 1 |
| 2 |
8
| ||
| 7 |
10
| ||
| 7 |
| ||
| 2 |
20
| ||
| 7 |
点评:本题考点是与圆有关的比例线段,考查圆周角与圆心角的关系,以及利用两角和与差的正弦公式求角的正弦,用正弦定理求三角形的边长,再利用三角形的面积公式求面积,本题涉及知识点较多,第二小题求解中综合利用解三角形的知识求面积,运算较繁,难度较大,做题时要用心体会本题转化的脉络.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 选做题
选做题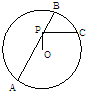 如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( )
如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( ) 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.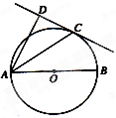 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
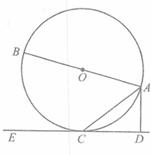
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.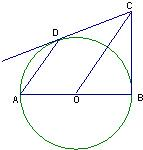 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.