题目内容
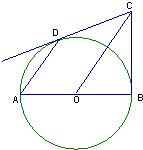如图，已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD，OA=2．（1）求证：DC是⊙O的切线；
（2）求AD•OC的值；
（3）若AD+OC=9，求CD的长．
分析：（1）连接OD，由BC是⊙O的切线得到∠B=90°，然后证明△OCD≌△OCB，得到∠ODC=90°，
（2）根据题干条件证明△ADB∽△ODC，得到AD•OC的值，
（3）在Rt△ODC中，利用勾股定理即可解得CD的长．
（2）根据题干条件证明△ADB∽△ODC，得到AD•OC的值，
（3）在Rt△ODC中，利用勾股定理即可解得CD的长．
解答：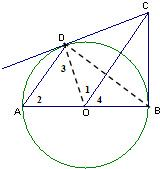
证明：（1）连接OD
∵BC是⊙O的切线，
∴∠B=90°
∵AD∥OC
∴∠1=∠3，∠2=∠4
∵OA=OD
∴∠2=∠3，
∴∠1=∠4
∵OB=OD，OC=OC
∴△OCD≌△OCB
∴∠ODC=90°
∴DC是⊙O的切线；
（2）连接BD，
∵△ADB∽△ODC
=
，
∴AD•OC=OD•AB=8．
（3）由（2）得AD•OC=8，与AD+OC=9联立解得AD=1，OC=8或AD=8，OC=1
由题意知，AD小于OC，
∴AD=1，OC=8符合题意
∴CD=
=2
．
证明：（1）连接OD∵BC是⊙O的切线，
∴∠B=90°
∵AD∥OC
∴∠1=∠3，∠2=∠4
∵OA=OD
∴∠2=∠3，
∴∠1=∠4
∵OB=OD，OC=OC
∴△OCD≌△OCB
∴∠ODC=90°
∴DC是⊙O的切线；
（2）连接BD，
∵△ADB∽△ODC
| AD |
| OD |
| AB |
| OC |
∴AD•OC=OD•AB=8．
（3）由（2）得AD•OC=8，与AD+OC=9联立解得AD=1，OC=8或AD=8，OC=1
由题意知，AD小于OC，
∴AD=1，OC=8符合题意
∴CD=
| 82-22 |
| 15 |
点评：本题考查了切线的判定，相似三角形的判定和性质等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．
练习册系列答案
相关题目
选做题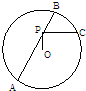
如图，已知AB是⊙O的一条弦，点P为AB上一点，PC⊥OP，PC交⊙O于C，若AP=4，PB=2，则PC的长是（ ）
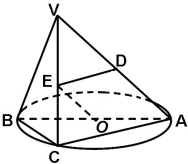如图，已知AB是⊙O的直径，点C是⊙O上的动点（异于A、B），过动点C的直线VC垂直于⊙O所在的平面，D，E分别是VA，VC的中点．
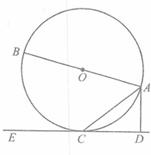
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．