题目内容
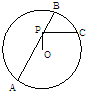 如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( )
如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( )| A、3 | ||
B、2
| ||
| C、2 | ||
D、
|
分析:由OP⊥PC,OP所在的直线过圆心,由垂径定理,我们可得PC为半弦长,延长CP后,根据相交弦定理,我们可以得到未知量PC与已知量AP、PB的关系,由此不难得到结论.
解答:解:如图,延长CP,交⊙O于D
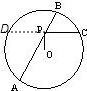 ∵PC⊥OP
∵PC⊥OP
由垂径定理可得:
PC=PD
由相交弦定理得:
PA•PB=PC•PD=PC2
又由AP=4,PB=2
∴PC=2
故选B
 ∵PC⊥OP
∵PC⊥OP由垂径定理可得:
PC=PD
由相交弦定理得:
PA•PB=PC•PD=PC2
又由AP=4,PB=2
∴PC=2
| 2 |
故选B
点评:本题考查的知识点,是相交弦定理,但切入点是由已知的条件,OP⊥PC,OP所在直线过圆心,这是垂径定理的前提条件,由此想到延长PC,构造出两条相交的弦,故熟练掌握相关定理,包括前提条件在内,是解决问题的捷径.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
 选做题
选做题 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.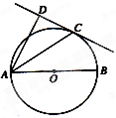 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
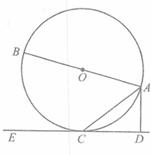
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.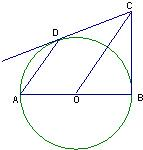 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.