题目内容
 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.(1)求证:直线ED⊥平面VBC;
(2)若VC=AB=2BC,求直线EO与平面VBC所成角大小的正切值.
分析:(1)由D、E分别为VA、VC的中点得到DE∥AC,由已知条件证出AC⊥平面VBC,从而问题得证;
(2)取BC的中点K,可得OK⊥平面VBC,则EK是斜线EO在平面VBC上的射影,∴∠OEK就是所求线面角的大小,然后解直角三角形克的结论.
(2)取BC的中点K,可得OK⊥平面VBC,则EK是斜线EO在平面VBC上的射影,∴∠OEK就是所求线面角的大小,然后解直角三角形克的结论.
解答: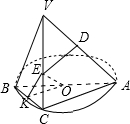 (1)证明:如图,
(1)证明:如图,
∵AB是⊙O的直径,∴AC⊥BC,
又∵VC垂直于⊙O所在的平面,∴AC⊥VC,
而BC∩VC=C,∴AC⊥平面VBC.
又∵D、E分别为VA、VC的中点,∴DE是△VCA的中位线,
∴DE∥AC,∴DE⊥平面VBC.
(2)解:设VC=AB=2BC=2a,取BC得重点K,
在正△OBC中,OK=
a,且OK∥AC,OK⊥平面VBC
∴EK是斜线EO在平面VBC上的射影,∴∠OEK就是所求线面角的大小,
而EK是RT△VBC的中位线,∴EK=
a,
∴tan∠OEK=
=
=
.
 (1)证明:如图,
(1)证明:如图,∵AB是⊙O的直径,∴AC⊥BC,
又∵VC垂直于⊙O所在的平面,∴AC⊥VC,
而BC∩VC=C,∴AC⊥平面VBC.
又∵D、E分别为VA、VC的中点,∴DE是△VCA的中位线,
∴DE∥AC,∴DE⊥平面VBC.
(2)解:设VC=AB=2BC=2a,取BC得重点K,
在正△OBC中,OK=
| ||
| 2 |
∴EK是斜线EO在平面VBC上的射影,∴∠OEK就是所求线面角的大小,
而EK是RT△VBC的中位线,∴EK=
| ||
| 2 |
∴tan∠OEK=
| OK |
| EK |
| ||||
|
| ||
| 5 |
点评:本题考查了直线与平面垂直的性质,考查了直线与平面所成的角,综合考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
 选做题
选做题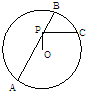 如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( )
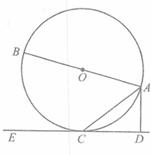
如图,已知AB是⊙O的一条弦,点P为AB上一点,PC⊥OP,PC交⊙O于C,若AP=4,PB=2,则PC的长是( )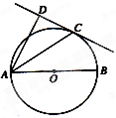 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.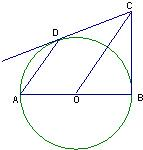 如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.
如图,已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD,OA=2.