题目内容
(本小题满分10分)经过点 ,倾斜角为
,倾斜角为 的直线
的直线 ,与曲线
,与曲线 :
: (
( 为参数)相交于
为参数)相交于 两点.
两点.
(1)写出直线 的参数方程,并求当
的参数方程,并求当 时弦
时弦 的长;[
的长;[
(2)当 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;
(3)当 时,求直线
时,求直线 的方程;
的方程;
(4)当 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程.
 ,倾斜角为
,倾斜角为 的直线
的直线 ,与曲线
,与曲线 :
: (
( 为参数)相交于
为参数)相交于 两点.
两点.(1)写出直线
 的参数方程,并求当
的参数方程,并求当 时弦
时弦 的长;[
的长;[(2)当
 恰为
恰为 的中点时,求直线
的中点时,求直线 的方程;
的方程;(3)当
 时,求直线
时,求直线 的方程;
的方程;(4)当
 变化时,求弦
变化时,求弦 的中点的轨迹方程.
的中点的轨迹方程. ,
,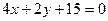
弦
 的中点的轨迹方程为
的中点的轨迹方程为 ;
;(1) 的参数方程
的参数方程 (
( 为参数). …………1分
为参数). …………1分
曲线 化为:
化为: ,将直线参数方程的
,将直线参数方程的 代入,得
代入,得

∵ 恒成立, ………………3分
恒成立, ………………3分
∴方程必有相异两实根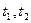 ,且
,且 ,
, .
.
∴
∴当 时,
时, . ………………5分
. ………………5分
(2)由 为
为 中点,可知
中点,可知 ,
,
∴ ,
,
故直线 的方程为
的方程为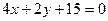 . ………………7分
. ………………7分
(3)∵ ,得
,得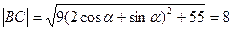
∴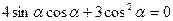 ,
,
∴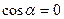 或
或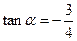
故直线 的方程为
的方程为 或
或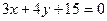 ………………9分
………………9分
(4)∵ 中点对应参数
中点对应参数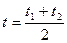
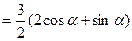
∴ (参数
(参数
 ),消去
),消去 ,得
,得
弦 的中点的轨迹方程为
的中点的轨迹方程为 ;
;
轨迹是以 为圆心,
为圆心, 为半径的圆. ………………10分
为半径的圆. ………………10分
 的参数方程
的参数方程 (
( 为参数). …………1分
为参数). …………1分曲线
 化为:
化为: ,将直线参数方程的
,将直线参数方程的 代入,得
代入,得 
∵
 恒成立, ………………3分
恒成立, ………………3分∴方程必有相异两实根
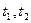 ,且
,且 ,
, .
.∴

∴当
 时,
时, . ………………5分
. ………………5分(2)由
 为
为 中点,可知
中点,可知 ,
,∴
 ,
,故直线
 的方程为
的方程为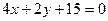 . ………………7分
. ………………7分(3)∵
 ,得
,得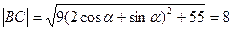
∴
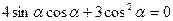 ,
,∴
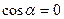 或
或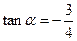
故直线
 的方程为
的方程为 或
或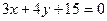 ………………9分
………………9分(4)∵
 中点对应参数
中点对应参数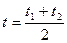
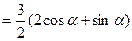
∴
 (参数
(参数
 ),消去
),消去 ,得
,得弦
 的中点的轨迹方程为
的中点的轨迹方程为 ;
;轨迹是以
 为圆心,
为圆心, 为半径的圆. ………………10分
为半径的圆. ………………10分
练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 的圆心在直线
的圆心在直线 上,经过点
上,经过点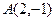 ,且与直线
,且与直线 相切,
相切,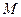 的方程;
的方程;  发出的光线经直线
发出的光线经直线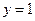 反射后可以照在圆
反射后可以照在圆
 已知关于x,y的方程C:
已知关于x,y的方程C: .
. ,求m的值。
,求m的值。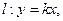 圆
圆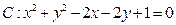 ,直线
,直线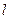 交圆于
交圆于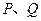 两点,点
两点,点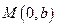 满足
满足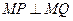 .
.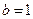 时,求
时,求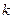 的值;
的值;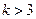 时,求
时,求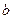 的取值范围.
的取值范围. 中,以
中,以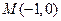 为圆心的圆与直线
为圆心的圆与直线 相切.
相切. 的方程;
的方程; 对称,求
对称,求 的值.
的值. 、
、 ,圆内的动点
,圆内的动点 满足
满足 ,求
,求 的取值范围.
的取值范围.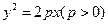 的准线与圆(
的准线与圆(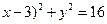 相切,则P的值为( )
相切,则P的值为( )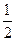
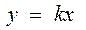 被圆
被圆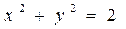 所截得的弦AB的长等于
所截得的弦AB的长等于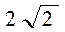
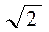
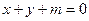 与圆
与圆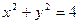 相切,则实数m的值为
相切,则实数m的值为
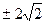


 )在圆
)在圆 外,则直线
外,则直线 与圆的位置关系是
与圆的位置关系是