题目内容
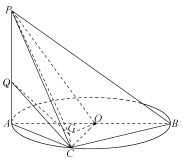
【题目】过双曲线![]() 的右焦点且垂直于
的右焦点且垂直于![]() 轴的直线与双曲线交于
轴的直线与双曲线交于![]() 两点,
两点,![]() 为虚轴的一个端点,且
为虚轴的一个端点,且![]() 为钝角三角形,则此双曲线离心率的取值范围为__________.
为钝角三角形,则此双曲线离心率的取值范围为__________.
【答案】![]()
【解析】分析:设出双曲线的左焦点,令x=﹣c,代入双曲线的方程,解得A,B的坐标,讨论∠DAB为钝角,可得![]() <0,或∠ADB为钝角,可得
<0,或∠ADB为钝角,可得![]() <0,运用向量数量积的坐标表示,再由离心率公式和范围,即可得到所求范围.
<0,运用向量数量积的坐标表示,再由离心率公式和范围,即可得到所求范围.
详解:设双曲线![]() 的左焦点F1(﹣c,0),
的左焦点F1(﹣c,0),
令x=﹣c,可得y=±![]() =±
=±![]() ,
,
可得A(﹣c,![]() ),B(﹣c,﹣
),B(﹣c,﹣![]() ),
),
又设D(0,b),可得![]() =(c,b﹣
=(c,b﹣![]() ),
),
![]() =(0,﹣
=(0,﹣![]() ),
),![]() =(﹣c,﹣b﹣
=(﹣c,﹣b﹣![]() ),
),
由△ABD为钝角三角形,可能∠DAB为钝角,可得![]() <0,
<0,
即为0﹣![]() (b﹣
(b﹣![]() )<0,
)<0,
化为a>b,即有a2>b2=c2﹣a2,
可得c2<2a2,即e=![]() <
<![]() ,
,
又e>1,可得1<e<![]() ,
,
可能△ADB中,∠ADB为钝角,可得![]() <0,
<0,
即为c2﹣(![]() +b)(
+b)(![]() ﹣b)<0,
﹣b)<0,
化为c4﹣4a2c2+2a4>0,
由e=![]() ,可得e4﹣4e2+2>0,
,可得e4﹣4e2+2>0,
又e>1,可得e>![]() .
.
综上可得,e的范围为(1,![]() )∪(
)∪(![]() .+∞).
.+∞).
故答案为:![]()

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: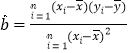 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
【题目】《中华人民共和国道路交通安全法》第47条规定:机动车行经人行横道时,应当减速慢行;遇到行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”.下表是某十字路口监控设备所抓拍的6个月内驾驶员不“礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
不“礼让斑马线”驾驶员人数 | 120 | 105 | 100 | 85 | 90 | 80 |
(Ⅰ)请根据表中所给前5个月的数据,求不“礼让斑马线”的驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)若该十字路口某月不“礼让斑马线”驾驶员人数的实际人数与预测人数之差小于5,则称该十字路口“礼让斑马线”情况达到“理想状态”.试根据(Ⅰ)中的回归直线方程,判断6月份该十字路口“礼让斑马线”情况是否达到“理想状态”?
(Ⅲ)若从表中3、4月份分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的两人恰好来自同一月份的概率.
参考公式:
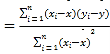 ,
,![]() .
.